Algorithms and Data Structures Course Notes

Posted May 3, 2024 Updated May 2, 2024

By 小文 153 min read

Week 1: Introduction

Logs

Consider a positive number \(y\), the logarithm of \(y\) to the base 2, written \(log_{2}\ y\) or just \(log\ y\), is the number of copies of \(2\) that must be multiplied together to equal \(y\).

\[\begin{align*} 2^0 & = 1 \\ 2^1 & = 2 \\ 2^2 & = 4 \\ 2^3 & = 8 \\ 2^4 & = 16 \\ 2^5 & = 32 \\ 2^6 & = 64 \\ 2^7 & = 128 \\ 2^8 & = 256 \\ 2^9 & = 512 \\ 2^{10} & = 1024 \\ \end{align*}\]

If \(y\) is not a power of \(2\), \(log\ y\) is a real number, meaning not a nice round integer.

\[\begin{align*} \log 5 & \approx 2.32 \\ \log 7 & \approx 2.81 \\ \log 9 & \approx 3.17 \\ \end{align*}\]

However we are really interested in roughly what the log of a number is. For example, we know \(log\ 4\) is \(2\), and \(log\ 8\) is \(3\), so \(log\ 5\) must be somewhere in between \(2\) and \(3\).

Logs in Java

Math.log refers to the natural \(log\) (i.e. \(ln\)) not \(log\) to the base 2. But we can calculate \(log_2\) from \(ln\):

\[log_2{(n)} = (ln\ n)/(ln\ 2)\]

Here’s a method to find \(log\ 2\) of a number:

  
//return log to the base 2 of a number
public static double log2(int n) {
    return Math.log(n) / Math.log(2);
}

Mathematical Properties of Logs

\[log\ 2^n = n\]

This is what \(log\) means.

\[log(xy) = log\ x + log\ y\]

If \(x=2^m\) and \(y=2^n\), then \(xy=2^m2^n=2^{m+n}\).

\[log(x/y) = log\ x - log\ y\]

In the same way, if \(x=2^m\) and \(y=2^n\), then \(x/y=2^m/2^n=2^{m-n}\).

Dividing Down to 1

How many times must we halve the value of a number \(n\) (discarding any remainders) to reach \(1\)?

Suppose that \(n\) is a power of \(2\):

\[8\rightarrow 4\rightarrow 2\rightarrow 1\]

\(8\) must be halved \(3\) times to reach \(1\).

If \(n=2^k\), \(n\) must be halved \(k\) times.

Suppose that \(n\) is not a power of \(2\):

\[9\rightarrow 4\rightarrow 2\rightarrow 1\]

\(9\) must be halved \(3\) times to reach \(1\).

\[15\rightarrow 7\rightarrow 3\rightarrow 1\]

\(15\) must be halved \(3\) times to reach \(1\).

If \(2^k < n < 2^{k+1}\), \(n\) must be halved \(k\) times.

We already know that if \(2^k < n < 2^{k+1}\), then \(log\ n\) is between \(k\) and \(k+1\), so roughly speaking we say that for any number \(n\), \(n\) must be divided by \(2\), \(log\ n\) times, to get down to \(1\).

Algorithms

An algorithm is a sequence of steps that solves a problem.

For example, consider the problem of multiplying two integers. There are many algorithms for solving this problem:

multiplication using a table (small integers only)
long multiplication
multiplication using logarithms
multiplication using a slide rule
binary multiplication (in computer hardware).

Example: finding a midpoint

Midpoint algorithm:

To find the midpoint of a given straight-line segment AB:

Draw intersecting circles of equal radius, centered at A and B respectively.
Let C and D be the points where the circles intersect.
Draw a straight line between C and D.
Let E be the point where CD intersects AB.
Terminate yielding E.

This algorithm can be performed by a human equipped with drawing instruments.

Example: computing a GCD

The greatest common divisor (GCD) of two positive integers is the largest integer that exactly divides both.

Euclid’s GCD algorithm:

To compute the GCD of positive integers m and n:

Set p to m, and set q to n.
While q does not exactly divide p, repeat:
1. Set p to q, and set q to (p modulo q).
Terminate yielding q.

  
static int gcd(int m, int n) {
    // Return the greatest common divisor of m and n
    // (assumed positive).
    int p = m, q = n;
    while (p % q != 0) {
        int r = p % q;
        p = q;
        q = r;
    }
    return q;
}

Data structures

A data structure is a way of organizing and storing a collection of data.

A static data structure is one whose capacity is fixed when it is first constructed, such as an array.

A dynamic data structure is one whose capacity is variable, so it can expand or contract at any time, such as a linked-list or binary-search-tree.

For each data structure we need algorithms for insertion, deletion, searching, etc.

Abstract Data Types (ADT)

When we write Java application code involving strings, we don’t care how strings are represented. We just declare String variables and manipulate them using String operations.

Similarly, when we write application code involving lists, we don’t care how lists are represented. We just declare List variables and manipulate them using List operations.

Similarly, when we write application code involving sets, we don’t care how sets are represented. We just declare Set variables and manipulate them using Set operations.

An abstract data type (ADT) is a data type whose representation is private, and therefore of no concern to the application code, such as String, List, Set.

Week 2: Algorithms and Complexity

Principles
Efficiency analysis
Complexity analysis
O-notation
Recursive algorithms

Principles

An algorithm is a step-by-step procedure for solving a stated problem. The algorithm will be performed by a processor. The processor may be human, mechanical, or electronic. The algorithm must be expressed in steps that the processor is capable of performing. The algorithm must eventually terminate, otherwise it will never yield an answer.

The algorithm must be expressed in some language that the processor “understands”. But the underlying algorithm is independent of the particular language chosen. The stated problem must be solvable, i.e., capable of solution by a step-by-step procedure.

Some interesting problems are unsolvable:

Can we devise an algorithm to determine whether a given program will terminate or not? i.e. A single algorithm for all program/input pairs. No such algorithm exists. This is Turing’s famous “halting problem”.

Efficiency analysis

Given a choice of algorithms for the same problem, which one is the best?

Depends on:

How much time does it require?
How much space (memory) does it require?
Is it feasible to use it at all?

Example:

As n increases, A’s time requirement grows faster than B’s, so algorithm B is better.

How should we measure time?

Measure time in seconds?

+ useful in practice
- dependent on programming language, compiler, processor speed

Count algorithm steps?

+ not dependent on compiler or processor speed
- dependent on the way the algorithm is expressed (few “big” steps vs many “small” steps)

Count characteristic operations?

+ dependent only on the algorithm itself
+ good measure of the algorithm’s intrinsic efficiency

Example: simple power algorithm

Simple power algorithm:

To compute \(b^n\):

Set \(p\) to \(1\).
For \(i = 1,…,n\), repeat:
1. Multiply \(p\) by \(b\).
Terminate yielding \(p\).

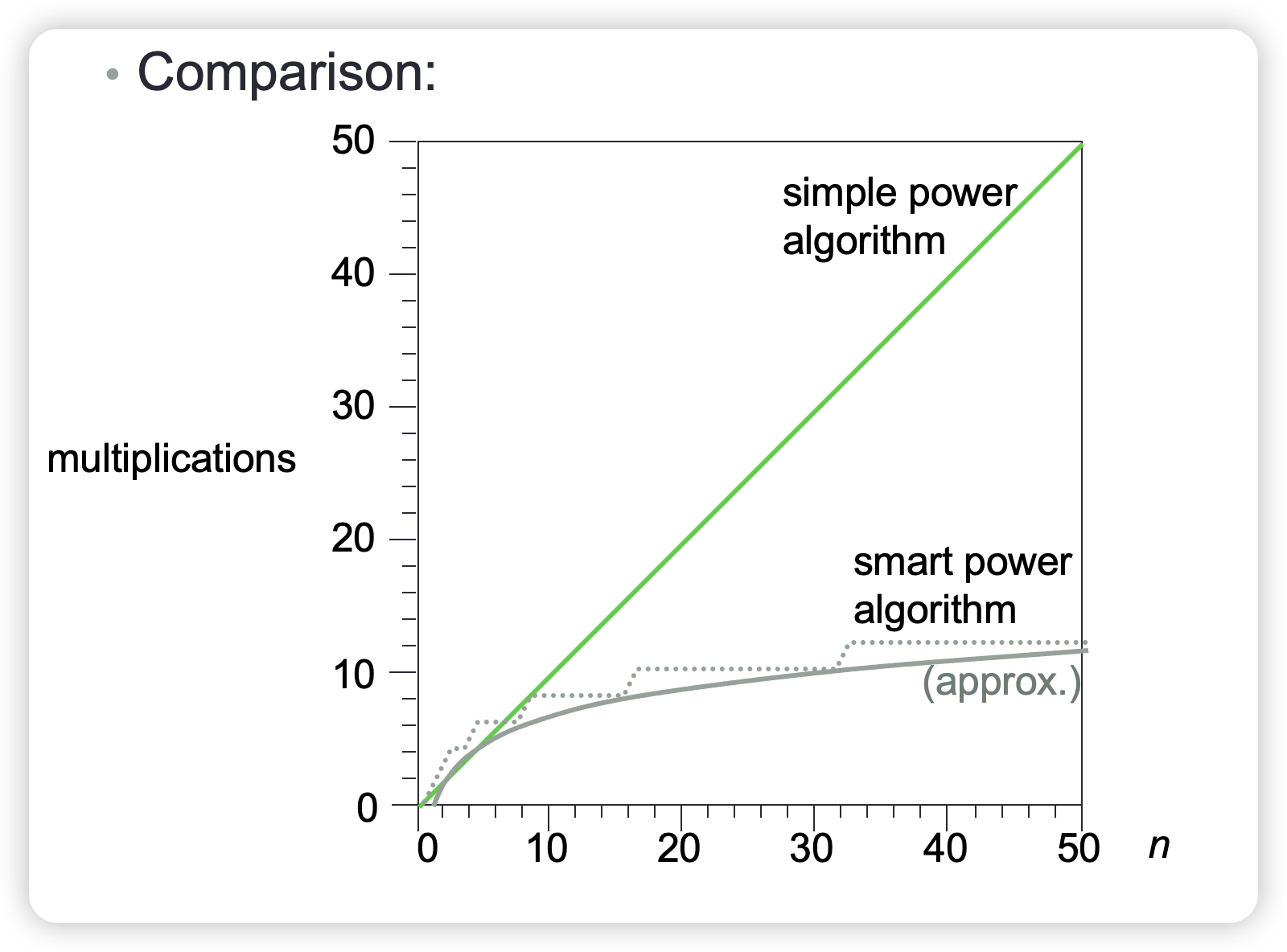
Analysis (counting multiplications):

Step 2.1 performs 1 multiplication. This step is repeated n times. The number of multiplications is \(n\).

For many interesting algorithms, the exact number of operations is too difficult to analyse mathematically. We can simplify the analysis by keeping the fastest-growing term but neglecting all slower-growing terms.

Example: smart power algorithm

The Idea: \(b^{1000}=b^{500} \cdot b^{500}\). If we know \(b^{500}\), we can compute \(b^{1000}\) with only 1 more multiplication.

Smart power algorithm:

To compute \(b^n\):

Set \(p\) to \(1\), set \(q\) to \(b\), and set \(m\) to \(n\).
While \(m > 0\), repeat:
1. If \(m\) is odd, multiply \(p\) by \(q\).
2. Halve \(m\), discarding any remainder.
3. Multiply \(q\) by itself.
Terminate yielding \(p\).

Analysis (Counting Multiplications):

Step 2.1 to 2.3 perform at most 2 multiplications, these steps are repeated as often as we must halve the value of n, discarding any remainders, until it reaches 0, it means, approximately \(log_2\ n+1\) times. Ignoring the insignificant 1, the max number of multiplication is approximately \(2\cdot log_2\ n\)

Complexity analysis

We can further simplify the analysis, by neglecting the constant factor in the fastest-growing term. The resulting formula is the algorithm’s time complexity. It focuses on the growth rate of the algorithm’s time requirement.

The number of multiplications for simple power algorithm is \(n\), time required is \(n\cdot t_{mult}\) where \(t_{mult}\) is the time required per multiplication, a constant. This is proportional to \(n\).

The complexity is of order n. This is written O(n) and referred to as big o of n.

The number of multiplications for smart power algorithm is \(2\cdot log_2\ n\) max, time required is \(2\cdot t_{mult}\cdot log_2\ n\). This is proportional to \(log_2\ n\).

The complexity is of order \(log_2\ n\). This is written O(log n).

O-notation

We have seen that O(log n) signifies a slower growth rate than O(n). So an O(log n) algorithm is inherently better than an O(n) algorithm, at least for large values of \(n\).

Complexity O(x) means “of order x,” i.e., growing proportional to x. Here x signifies the growth rate, neglecting slower-growing terms and constant factors.

Important explanations:

Slower-growing terms: these are the parts of the expression that increase at a relatively slower rate as the input size (n) increases. For example, consider an algorithm that takes \(2n + 3\) steps to complete. Here, \(2n\) and \(3\) are both terms. As \(n\) gets larger, the term \(2n\) increases much faster than the constant \(3\). Hence, \(3\) is considered a slower-growing term compared to \(2n\).

Fastest-growing term: this is the term within the expression that increases at the highest rate as the input size grows. Continuing with the previous example, \(2n\) is the fastest-growing term. When deciding the overall complexity of the algorithm, we’re mostly interested in this term because it dominates the behavior of the function for large values of \(n\). The other terms become less significant as \(n\) grows.

When we analyze algorithms using big O notation, we focus on the fastest-growing term and disregard the slower-growing terms and any constant factors. This is because, for large inputs, the impact of these smaller terms becomes negligible. For instance, both \(2n + 3\) and \(100n + 6\) have the same big O complexity of O(n), because we’re primarily concerned with how the algorithm scales with n, and in both cases, it’s linearly.

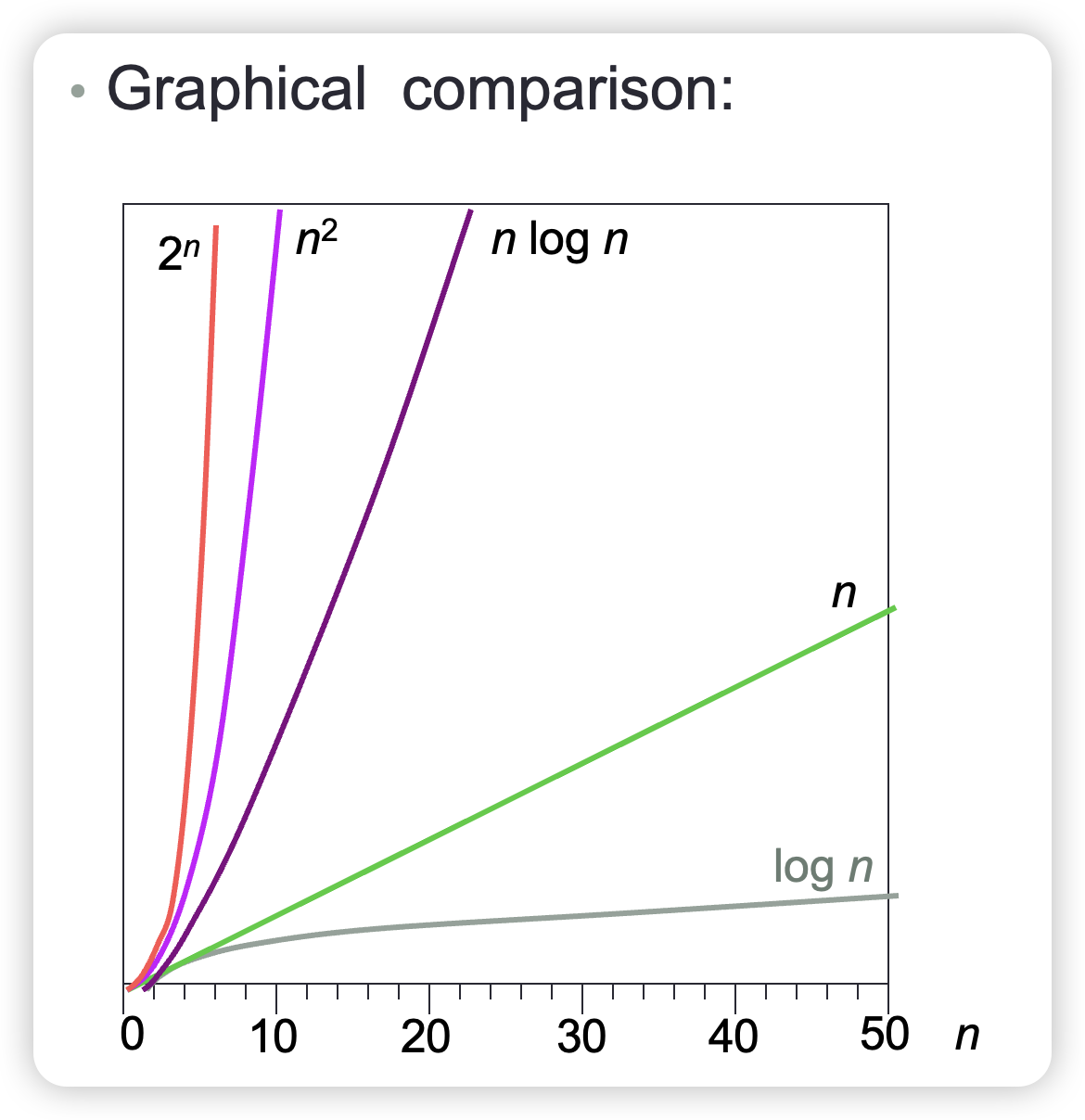
Common time complexities:

Time Complexity	Description	Feasibility
\(O(1)\)	Constant Time	Feasible
\(O(log\ n)\)	Logarithmic Time	Feasible
\(O(n)\)	Linear Time	Feasible
\(O(n\ log\ n)\)	Log Linear Time	Feasible
\(O(n^2)\)	Quadratic Time	Often Feasible
\(O(n^3)\)	Cubic Time	Less Often Feasible
\(O(2^n)\)	Exponential Time	Rarely Feasible

Recursive algorithms

A recursive algorithm is an algorithm in which at least one step is a “call” to itself. Sometimes a problem can be solved either by an iterative algorithm or by a recursive algorithm. The recursive version tends to be:

+ more elegant and easier to understand
– less efficient (extra calls consume time and space).

Sometimes a problem can be solved only by a recursive algorithm.

When does recursion work?

Given a recursive algorithm, how can we sure that it terminates?

The algorithm must have:

at least one “easy” case
at least one “hard” case

In an “easy” case, the algorithm must terminate without calling itself. In a “hard” case, the algorithm may call itself, but only to deal with an “easier” case.

Example:

Factorial: calculate \(n! = n \times (n-1) \times (n-2) \times … 1\)

if \(n =1\), return \(1\)
else, return \(n \times (n-1)!\)

Power: calculate \(m^n\)

if \(n = 0\), return \(1\)
else, return \(m \times m^{n-1}\)

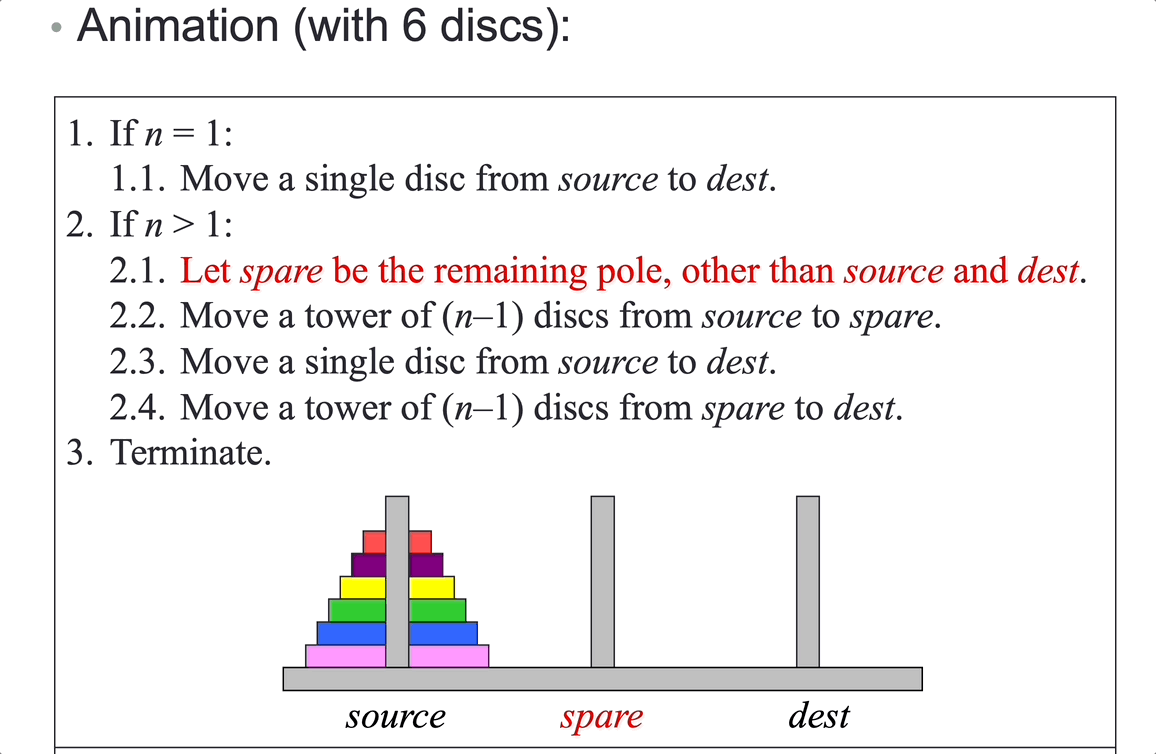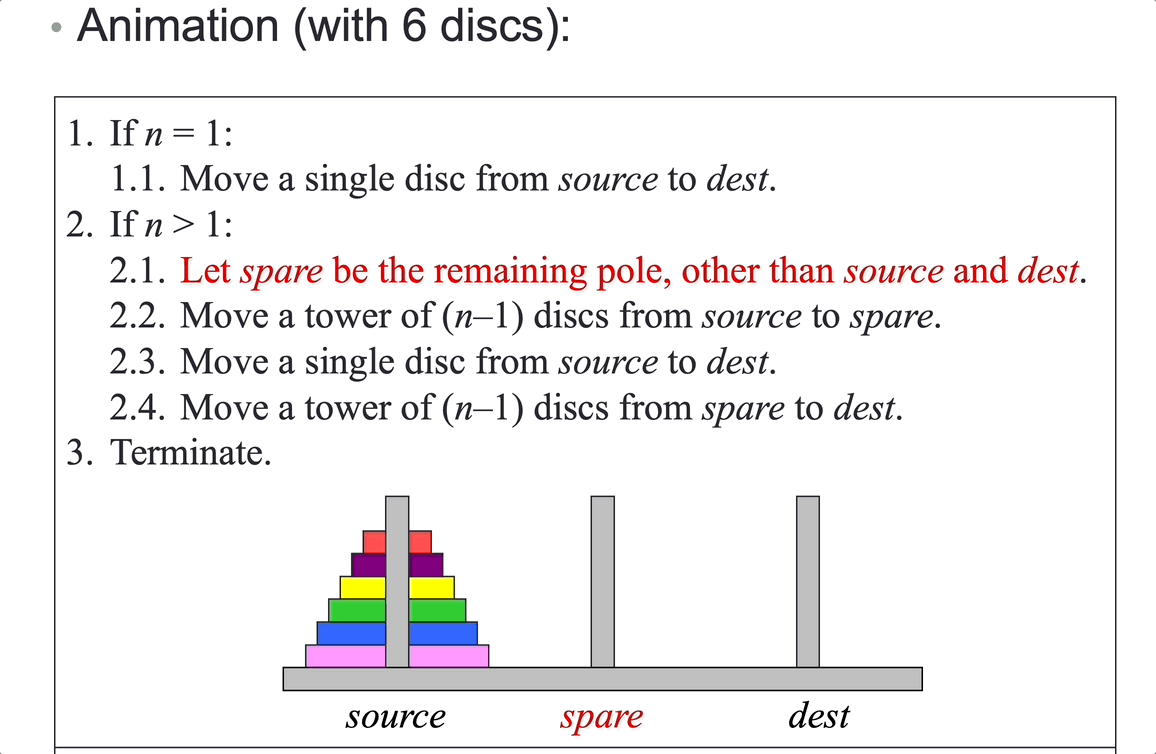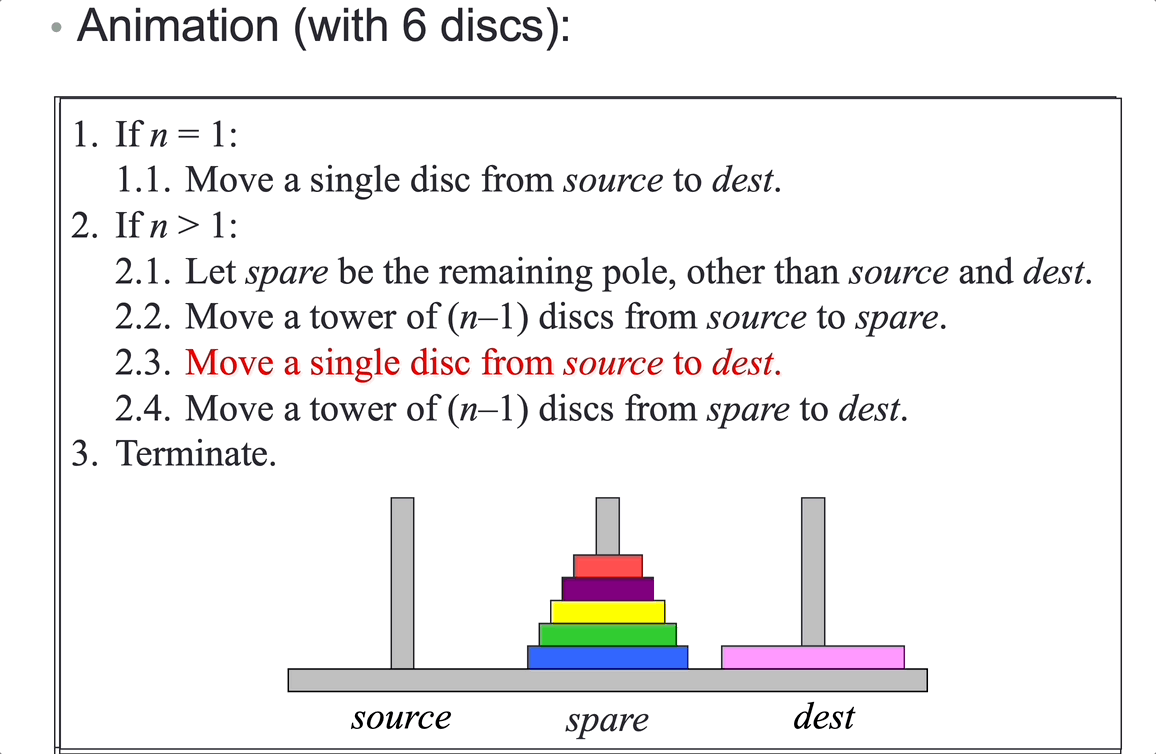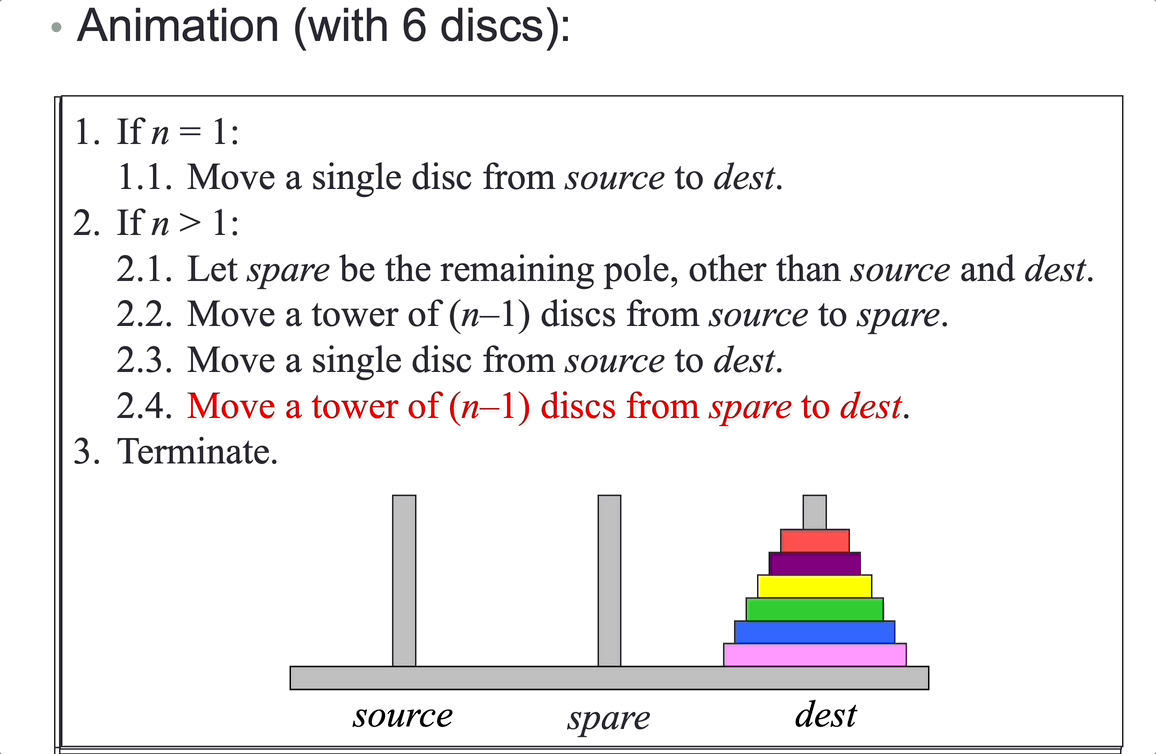
Tower of Hanoi: move \(n\) disks from peg A to peg C, using peg B as an auxiliary.

Analysis (counting moves):

Let the total number of moves required to move a tower of n discs be moves(n). Then:

\[moves(n) = 2^n – 1\]

Time complexity is \(O(2^n)\).

Additional material:

How to Calculate Big O

Week 3: Arrays

Properties
Insertion
Deletion
Searching: linear search, binary search
Merging
Sorting: selection sort, merge-sort, quick-sort

Properties

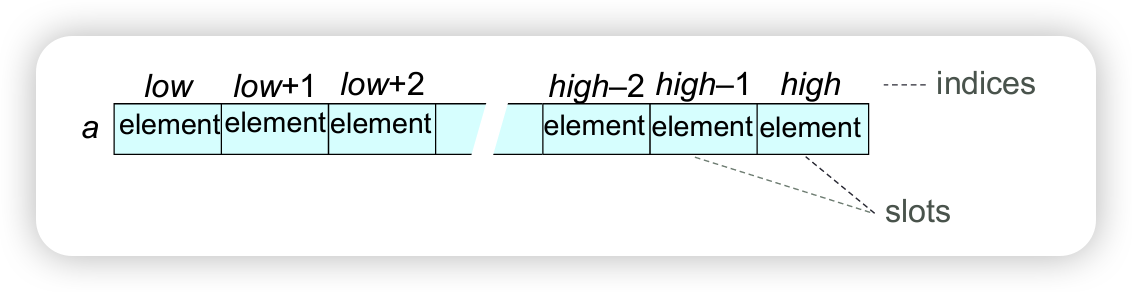
An array is a sequence of slots. Each slot contains an element, value or object. Each slot has a fixed index. The indices are consecutive integers.

An array’s length is the number of slots. The length is fixed when the array is constructed. Any array slot can be efficiently accessed, using its index, in O(1) time, this is a constant time operation.

Subarrays

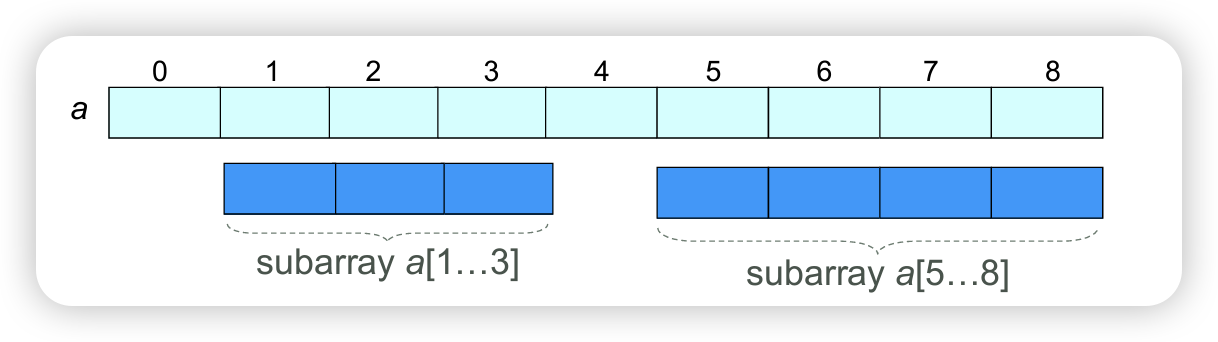
A subarray of an array A is a sequence of consecutive slots in A.

Notation:

A[l…r] is the subarray of A that comprises slots A[l], A[l+1],…, A[r].
subarray notation may be used to express algorithms, but it is not directly supported by Java.

subarray A[l…r] has length \(r-l+1\).

Sorted Arrays

A (sub)array is sorted if its elements are in ascending order, each element is less than or equal to the element on its right. The meaning of “less” must be defined for each data type.

for numbers: “x is less than y” means that x is numerically smaller than y, i.e., \(x<y\).
for strings: “x is less than y” conventionally means that x lexicographically precedes y. E.g., “bat” is less than “bath,” which in turn is less than “bay.”

Java’s `Comparable` Interface

The following interface from java.util captures this notion:

  
public interface Comparable {
    public int compareTo(Object that);
    // Return a negative integer if this object is less than that, or zero if
    // if this object is equal to that, or a positive integer if this object is greater
    // than that.
}

If a class Thing implements Comparable, it must define the compareTo method in accordance with the above contract:

  
public class Thing implements Comparable<Thing> {
    // Class implementation details go here...

    @Override
    public int compareTo(Thing that) {
        // Return a negative integer if this thing is less than that,
        // or zero if this thing is equal to that,
        // or a positive integer if this thing is greater than that.
        // Implement the comparison logic here.
    }
}

This captures the notion of “less” and “greater” for objects of class Thing. String, Integer, etc. implement Comparable.

Java.util.Arrays contains various methods for working with arrays, including sorting, see the Java API documentation.

Next we are going to implement the insert, search and sort algorithms ourselves and understand how they work under the hood.

Insertion

Problem: given a (sub)array a[left…right], insert an element elem in the slot a[ins]. If necessary, shift elements to make way for it.

Array insertion algorithm:

To insert elem at index ins in a[left…right] where left <= ins <= right:

Copy a[ins…right-1] into a[ins+1…right]: shift elements one slot to the right.
Copy elem into a[ins].
Terminate.

Analysis (counting copies):

Let n = right - left + 1 be the length of the array. Step 1 performs between 0 and n-1 copies. On average it performs (n-1)/2 copies. Step 2 performs 1 copy. Average number of copies is:

\[\frac{0+1+2+3+…+(n-1)}{n} + 1= \frac{\frac{n(n-1)}{2}}{n} + 1 = \frac{n-1}{2} + 1 = \frac{1}{2}\cdot n + \frac{1}{2}\]

Time complexity is O(n).

Deletion

Problem: given a (sub)array a[left…right], delete the element at index del. If necessary, shift elements to fill the gap.

Array deletion algorithm:

To delete the element ad index del in a[left…right] where left <= del <= right:

Copy a[del+1…right] into a[del…right-1]: shift elements one slot to the left.
Make a[right] null.
Terminate.

Analysis (counting copies):

Let n = right - left + 1 be the length of the array. Step 1 performs between 0 and n-1 copies. On average it performs (n-1)/2 copies. Step 2 performs 1 copy. Average number of copies is:

\[\frac{0+1+2+3+…+(n-1)}{n} + 1= \frac{\frac{n(n-1)}{2}}{n} + 1 = \frac{n-1}{2} + 1 = \frac{1}{2}\cdot n + \frac{1}{2}\]

Time complexity is O(n), which is linear.

Searching

Problem: given a (sub)array a[left…right], search for an element elem.

Choice of algorithm:

linear search (unsorted or sorted array)
binary search (sorted array)

Linear Search

Linear search algorithm:

To find which (if any) element of a[left…right] equals elem:

For p = left,…,right, repeat:
1. If a[p] equals elem, terminate yielding p.
Terminate yielding null.

Analysis:

Let n = right - left + 1 be the length of the array.

If the search is unsuccessful, step 1.1 is repeated n times. The number of comparisons is n.

If the search is successful, step 1.1 is repeated between 1 and n times. The average number of comparisons is:

\[(1+2+3+…+n)/n = n/2\]

In either case, the time complexity is O(n).

Implementation in Java:

  
static <E> int linearSearch(E target, E[] a, int left, int right) {
    // Find which (if any) element of a[left…right]
    // equals target.
    for (int p = left; p <= right; p++) {
        if (target.equals(a[p])) {
            return p;
        }
    }
    return -1;
}

Binary Search

Assume now that we are searching a sorted (sub)array. Consider searching a dictionary for a target word:

bad idea: look at page 1, then page 3, until you find the page containing the target word.
better idea: choose a page near the middle, if the target word happens to be on that middle page, you’re finished. If the target word is less or greater than the words on that middle page, and repeat. This is binary search.

Binary search algorithm:

To find which (if any) element of the sorted (sub)array a[left…right] equals target:

Set l = left, and set r = right.
While l <= r, repeat:
1. Let m be an integer about midway between l and r.
2. If a[m] equals target, terminate yielding m.
3. If target is less than a[m], set r = m-1.
4. If target is greater than a[m], set l = m+1.
Terminate yielding null.

Analysis (counting comparisons):

n is the length of the array. Assume steps 2.2-4 perform 1 comparison. If the search is unsuccessful, these steps are repeated as often as we must have n to reach 0, so the number of comparisons is \(log_2\ n + 1\).

If the search is successful, these steps are repeated at most \(log_2\ n + 1\) times.

In either case, the time complexity is O(log n).

Implementation in Java:

  
public static <E extends Comparable<E>> int binarySearch(
    E target,
    E[] a,
    int left,
    int right) {

    // Find which (if any) element of the sorted (sub)array
    // a[left…right] equals target.
    int l = left;
    int r = right;

    while (l <= r) {
        int m = (l + r) / 2; // roughly middle
        int comp = target.compareTo(a[m]);

        if (comp == 0) {
            return m;
        } else if (comp < 0) {
            r = m - 1; // move right boundary up
        } else {
            l = m + 1; // move left boundary down
        }
    }

    return -1; // target not found
}

Comparison of searching algorithms

Algorithm	No. of comparisons	Time complexity
Linear search (unsorted array)	~ n/2 (successful) n (unsuccessful)	O(n)
Linear search (sorted array)	~ n/2	O(n)
Binary search (sorted array)	~ log₂ n	O(log n)

Merging

Problem: given two sorted arrays, make a third sorted array containing a copy of all elements of the two original arrays.

Ideas: compare the leftmost elements of the two arrays. Whichever element is less, copy it into the third array, and thereafter ignore that element.

Array merging algorithm:

To merge a1[left1…right1] and a2[left2…right2] into a3[left3…right3] where both a1 and a2 are sorted:

Set i = left1, set j = left2, and set k = left3.
While i <= right1 and j <= right2, repeat:
1. If a1[i] is less than or equal to a2[j], copy a1[i] into a3[k], and increment i and k.
2. Otherwise, copy a2[j] into a3[k], and increment j and k.
If i <= right1, copy a1[i…right1] into a3[k…right3].
If j <= right2, copy a2[j…right2] into a3[k…right3].
Terminate.

Analysis (counting copies):

Let \(n_1\) and \(n_2\) be the lengths of a1 and a2, \(n = n_1 + n_2\).

Each element of a1 is copied once, and each element of a2 is copied once. So the number of copies is \(n_1 + n_2 = n\).

Time complexity is O(n).

Analysis (counting comparisons):

Let \(n_1\) and \(n_2\) be the lengths of a1 and a2, \(n = n_1 + n_2\).

Assume steps 2.1-2 perform a single comparison. Steps 2.1-2 are repeated at most \(n-1\) times. The maximum number of comparisons is \(n-1\).

Time complexity is again O(n).

Java implementation:

  
public static <E extends Comparable<E>> void merge(
    E[] a1, int l1, int r1,
    E[] a2, int l2, int r2,
    E[] a3, int l3) {

    // Merge the sorted subarrays a1[l1 - r1] and
    // a2[l2 – r2] into a3[l3]
    int i = l1, j = l2, k = l3;

    while (i <= r1 && j <= r2) {
        int comp = a1[i].compareTo(a2[j]);
        if (comp <= 0) {
            a3[k++] = a1[i++];
        } else {
            a3[k++] = a2[j++];
        }
    }

    while (i <= r1) {
        a3[k++] = a1[i++];
    }

    while (j <= r2) {
        a3[k++] = a2[j++];
    }
}

Sorting

Problem: given an unsorted array, rearrange its elements into ascending order.

Selection Sort

Ideas: find the least element in the array, swap it into the leftmost slot. Repeat this, now ignoring the leftmost slot.

Selection sort algorithm:

To sort a[left…right] into ascending order:

For l = left,…,right-1, repeat:
1. Let p such that a[p] is the least of a[l…right].
2. If p != l, swap a[p] and a[l].
Terminate.

Analysis (counting comparisons):

Let n = right - left + 1 be the length of the array. Step 1.1 performs right-l comparisons. This is repeated with l = left,…,right-1, so the total number of comparisons is:

\[(right - left) + (right - left - 1) + … + 1 = \frac{n(n-1)}{2} = \frac{n^2}{2} - \frac{n}{2}\]

Time complexity is \(O(n^2)\).

Implementation in Java:

  
public static <E extends Comparable<E>> void sort(E[] a, int left, int right) {
    // Sort a[left…right] into ascending order
    for (int l = left; l < right; l++) {
        // Note: l is the starting index, not a letter; 1 is not used.
        int p = l;          // Initialize p to current left index
        E least = a[p];     // Assume the first element is the smallest

        // Find the smallest element in the unsorted portion
        for (int k = l + 1; k <= right; k++) {
            int comp = a[k].compareTo(least);
            if (comp < 0) {
                p = k;      // Update p to the index of the smallest found
                least = a[p];
            }
        }

        // Swap the found minimum element with the first element of the unsorted portion
        if (p != l) {
            a[p] = a[l];
            a[l] = least;
        }
    }
}

Merge Sort

The divide-and-conquer strategy is effective for solving many problems. To solve a “hard” problem, break the problem down into two or more “easier” sub-problems, solve these sub-problems separately, then combine their answers. The divide-and-conquer strategy naturally suggests a recursive algorithm.

Ideas: divide the array into two halves, sort each half, then merge the two sorted halves.

Merge-sort algorithm:

To sort a[left…right] into ascending order:

If left < right:
1. Let mid be the integer about midway between left and right.
2. Sort a[left…mid] into ascending order.
3. Sort a[mid+1…right] into ascending order.
4. Merge a[left…mid] and a[mid+1…right] into auxiliary array b
5. Copy all elements of b into a[left…right].
Terminate.

Analysis (counting comparisons):

Let n = right - left + 1 be the length of the array.

Let the total number of comparisons required to sort a (sub)array of length m be comps(m).

Step 1.2 takes about comps(n/2) comparisons to sort the left subarray. Step 1.3 takes about comps(n/2) similarly. Step 1.4 takes about n-1 comparisons to merge the subarray.

Therefore, comps(n) is about 2*comps(n/2) + n-1 if n > 1, comps(n) is 0 if n <= 1.

Time complexity is O(n log n).

Space complexity is O(n), since step 1.4 needs an auxiliary array of length n.

Note: The time complexity of merge sort is O(n log n), which is better than the time complexity of selection sort, O(n^2), for large values of n.

Implementation in Java:

  
public class MergeSort {
    public static <E extends Comparable<E>> void merge(
            E[] a1, int l1, int r1, E[] a2, int l2, int r2, E[] a3, int l3) {
        // Merge the sorted subarrays a1[l1 r1] and
        // a2[l2 r2] into a3[l3].
        int i = l1, j = l2, k = l3;
        while (i <= r1 && j <= r2) {
            int comp = a1[i].compareTo(a2[j]);
            if (comp <= 0) a3[k++] = a1[i++];
            else a3[k++] = a2[j++];
        }
        while (i <= r1) a3[k++] = a1[i++];
        while (j <= r2) a3[k++] = a2[j++];
    }

    public static <E extends Comparable<E>> void mergeSort(E[] a, int l1, int r1) {
        if (l1 < r1) {
            int m = (l1 + r1) / 2;
            mergeSort(a, l1, m);
            mergeSort(a, m + 1, r1);
            @SuppressWarnings("unchecked")
            E[] b = (E[]) new Comparable[r1 - l1 + 1];
            merge(a, l1, m, a, m + 1, r1, b, 0);
            for (int i = l1; i <= r1; i++) a[i] = b[i - l1];
        }
    }

    public static <E extends Comparable<E>> String printArray(E[] a) {
        String s = "";
        for (E e : a) s += e + ",";
        return s;
    }

    /**
     * @param args
     */
    public static void main(String[] args) {
        Integer[] a = {4, 3, -1, 2, 17, 2, 0, 4, 5};
        mergeSort(a, 0, 8);
        System.out.println(printArray(a));
    }
}

Quick Sort

Ideas: choose any element (called the pivot). Then partition the array into three subarray such that the left subarray contains only elements less than or equal to the pivot, the middle subarray contains only the pivot, the right subarray contains only elements greater than or equal to the pivot. Finally sort the left subarray and the right subarray separately.

Quick-sort algorithm:

To sort a[left…right] into ascending order:

If left < right:
1. Partition a[left…right] such that:
  - a[left…p-1] are all less than or equal to a[p], a[p] now contains the pivot
  - a[p+1…right] are all greater than or equal to a[p]
2. Sort a[left…p-1] into ascending order.
3. Sort a[p+1…right] into ascending order.
Terminate.

Under the hood:

Analysis (counting comparisons):

Let n be the length of the array. Let the total number of comparisons required to sort a (sub)array of length m be comps(m). Assume that step 1.1 takes about n-1 comparisons to partition the array.

In the best case, the pivot always turns out to be the median element. So the left and right subarray both have length about n/2. Step 1.2 and 1.3 perform about comps(n/2) comparisons each.

Therefore, comps(n) is about n-1 + 2*comps(n/2) if n > 1, comps(n) is 0 if n <= 1.

Best-case time complexity is O(n log n).

In the worst case, the pivot always turns out to be the smallest element. So the right subarray has length n-1 whilst the left subarray is empty. Step 1.3 performs comps(n-1) comparisons, but step 1.2 does nothing.

Therefore, comps(n) is about n-1 + comps(n-1) if n > 1, comps(n) is 0 if n <= 1.

Worst-case time complexity is O(n^2).

This case arises if the array is already sorted.

Implementation in Java:

  
public class QuickSort {
    public static <E extends Comparable<E>> int partition(E[] a, int left, int right) {
        int p = left;
        E pivot = a[left];
        for (int r = left + 1; r <= right; r++) {
            if (a[r].compareTo(pivot) < 0) {
                a[p] = a[r];
                a[r] = a[p + 1];
                a[p + 1] = pivot;
                p++;
            }
        }
        return p;
    }

    public static <E extends Comparable<E>> void quickSort(E[] a, int left, int right) {
        if (left < right) {
            int p = partition(a, left, right);
            quickSort(a, left, p - 1);
            quickSort(a, p + 1, right);
        }
    }

    public static <E extends Comparable<E>> String printArray(E[] a) {
        String s = "";
        for (E e : a) s += e + ",";
        return s;
    }

    /**
     * @param args
     */
    public static void main(String[] args) {
        Integer[] a = {4, 3, -1, 2, 11, 2, 0, 4, 5};
        quickSort(a, 0, 8);
        System.out.println(printArray(a));
    }
}

Quick-sort partition algorithm:

To partition a[left…right] such that a[left…p-1] are all less than or equal to a[p], and a[p+1…right] are all greater than or equal to a[p]:

Let pivot be the element in a[left], and set p=left.
For r=left+1,…,right, repeat:
1. If a[r] is less than pivot,
  1. Copy a[r] into a[p], a[p+1] into a[r], and pivot into a[p+1].
  2. Increment p.
Terminate yielding p.

Comparison of sorting algorithms

Algorithm	No. of comparisons	No. of copies	Time complexity	Space complexity
Selection sort	n²/2	2n	O(n²)	O(1)
Insertion sort	n²/4	n²/4	O(n²)	O(1)
Merge-sort	n log₂n	2n log₂n	O(n log n)	O(n)
Quick-sort (best)	n log₂n	2n/3 log₂n	O(n log n)	O(log n)
Quick-sort (worst)	n²/2	0	O(n²)	O(n)

Week 4 - Linked Lists

Linked-list: singly linked-lists, doubly linked-lists
Insertion
Deletion
Searching

Linked Lists

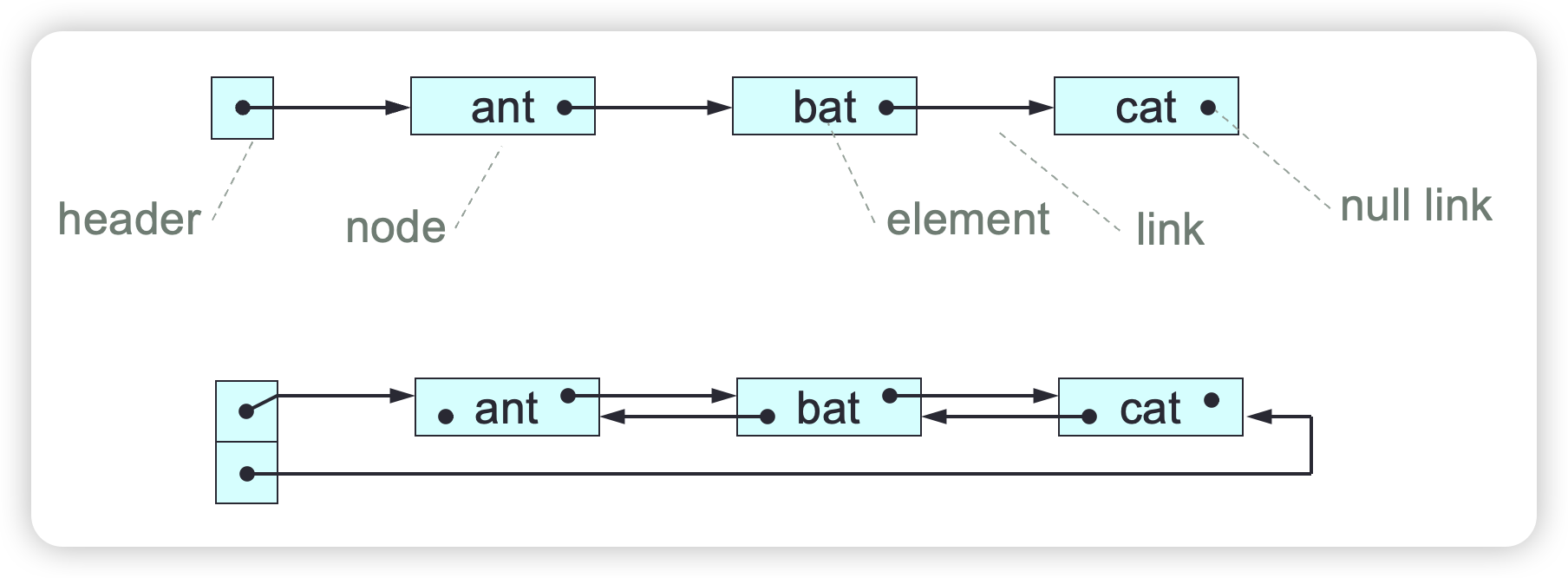
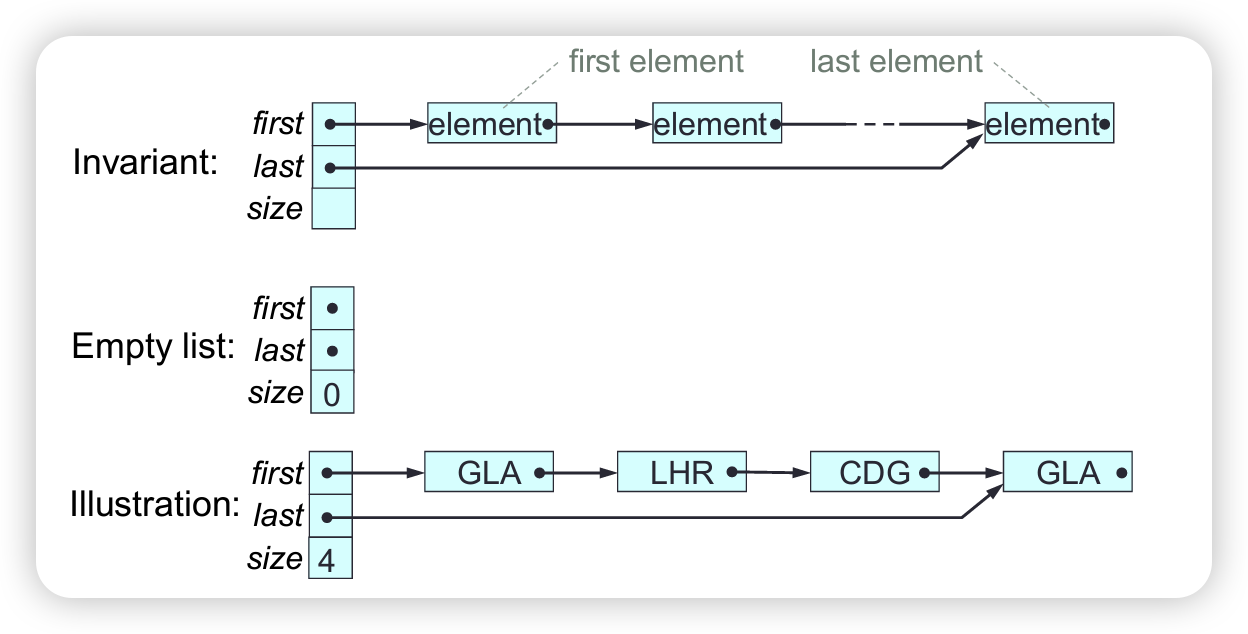
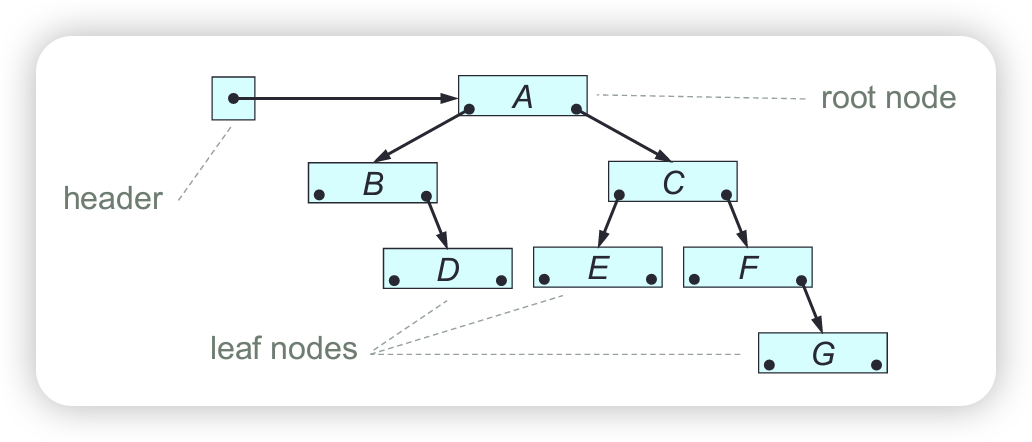
A linked-list consists of a header together with a sequence of nodes connected by links. Each node (except the last) has a next node. Each node (except the first) has a predecessor node. Each node contains a single element (value or object), plus links to its next and/or predecessor.

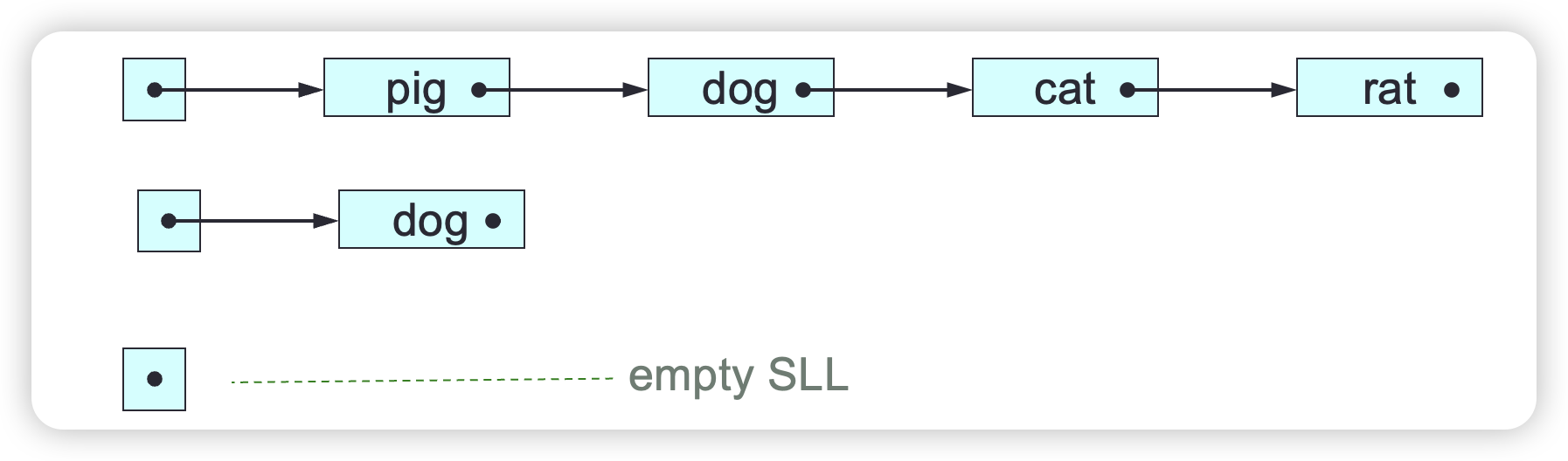
The length of a linked-list is its number of nodes. An empty linked-list has no nodes. We can manipulate a linked-list’s elements. We can also manipulate a linked-list’s links, and thus change its structure, whereas an array’s structure can’t be changed.

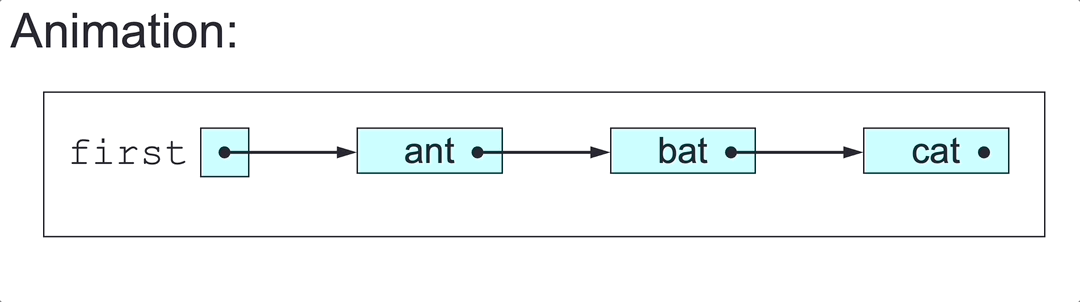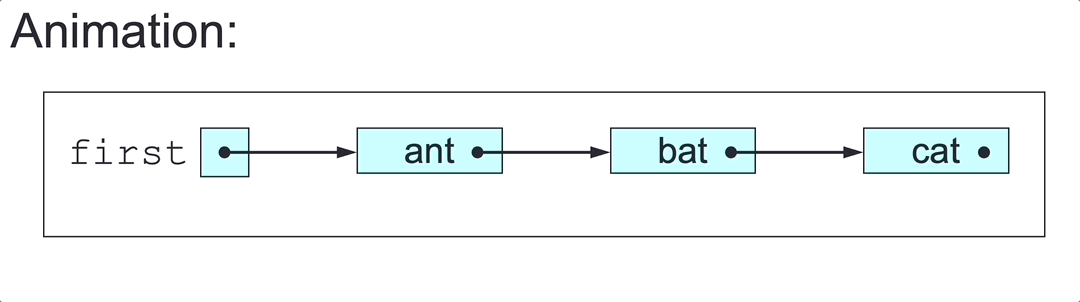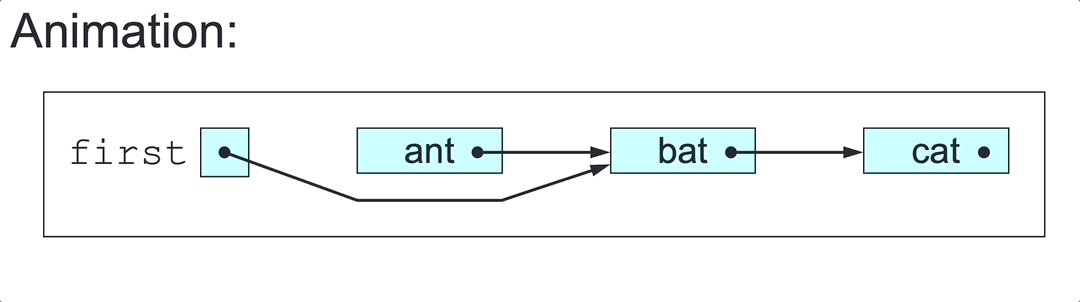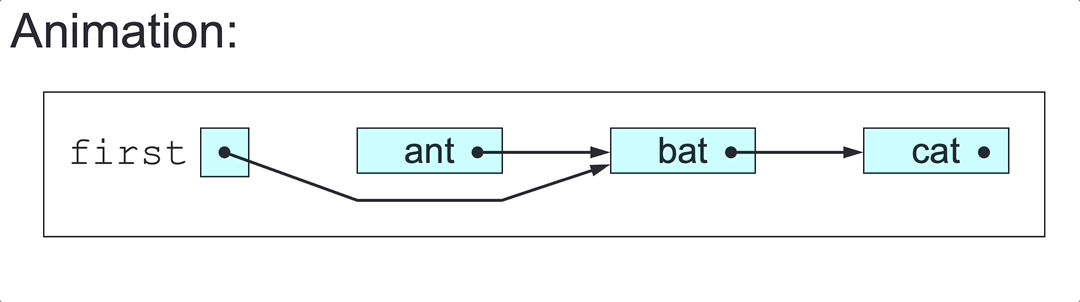
Singly Linked Lists

A singly linked list (SLL) consists of a header together with a sequence of nodes connected by links in one direction only.

Each SLL node contains a single element, plus a link to the node’s next node or null if the node has no next node. The SLL header contains a link to the SLLs’ first node or a null link if the SLL is empty.

  
public class SLL<E> { // Each SLL object is the header of a singly-linked-list.
    private Node<E> first;

    public SLL() { // Construct an empty SLL.
        first = null;
    }

    ////////// Inner class //////////
    private static class Node<E> { // Each Node object is a node of a singly-linked-list.
        protected E element;
        protected Node<E> next;

        public Node(E elem, Node<E> n) {
            element = elem;
            next = n;
        }
    }

    public void printFirstToLast() { // Print all elements in this SLL, in first-to-last order.
        Node<E> curr = first;
        while (curr != null) {
            System.out.println(curr.element);
            curr = curr.next;
        }
    }
}

To delete a SLL’s first node (in class SLL):

  
public void deleteFirst () {
    // delete this SLL's first node, assuming length > 0
    first = first.next;
}

SLL Insertion

Problem: insert a new element at a given point in a linked-list.

Four cases to consider:

insertion in an empty linked-list
insertion before the first node of a non-empty linked-list
insertion after the last node of a non-empty linked-list
insertion between nodes of a non-empty linked-list

The insertion algorithm needs links to the new node’s successor and predecessor.

SLL insertion algorithm:

To insert elem at a given point in the SLL headed by first:

Make ins a link to a newly created node with element elem.
If the insertion point is before the first node:
1. Set ins’s next node to first.
2. Set first to ins: case 1 and 2
Else, if the insertion point is after the node pred:
1. Set ins’s next node to pred’s next node.
2. Set pred’s next node to ins: case 3 and 4
Terminate.

  
public void insert(E elem, Node<E> pred) {
    // Insert elem at a given point in this SLL, either after the
    // node pred, or before the first node if pred is null.
    Node<E> ins = new Node<>(elem, null);

    if (pred == null) {
        ins.next = first;
        first = ins;
    } else {
        ins.next = pred.next;
        pred.next = ins;
    }
}

SLL Deletion

Problem: delete a given node from a linked-list.

Four cases to consider:

deletion of a singleton node.
deletion of the first but not last node.
deletion of the last but not first node.
deletion of an intermediate node.

The deletion algorithm needs links to the deleted node’s successor and predecessor.

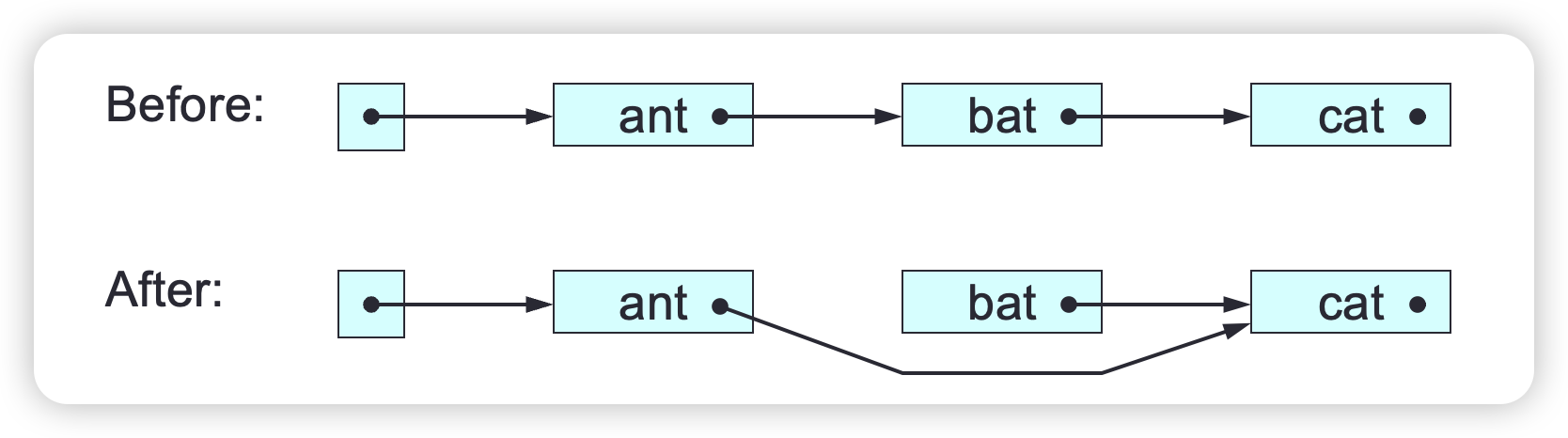
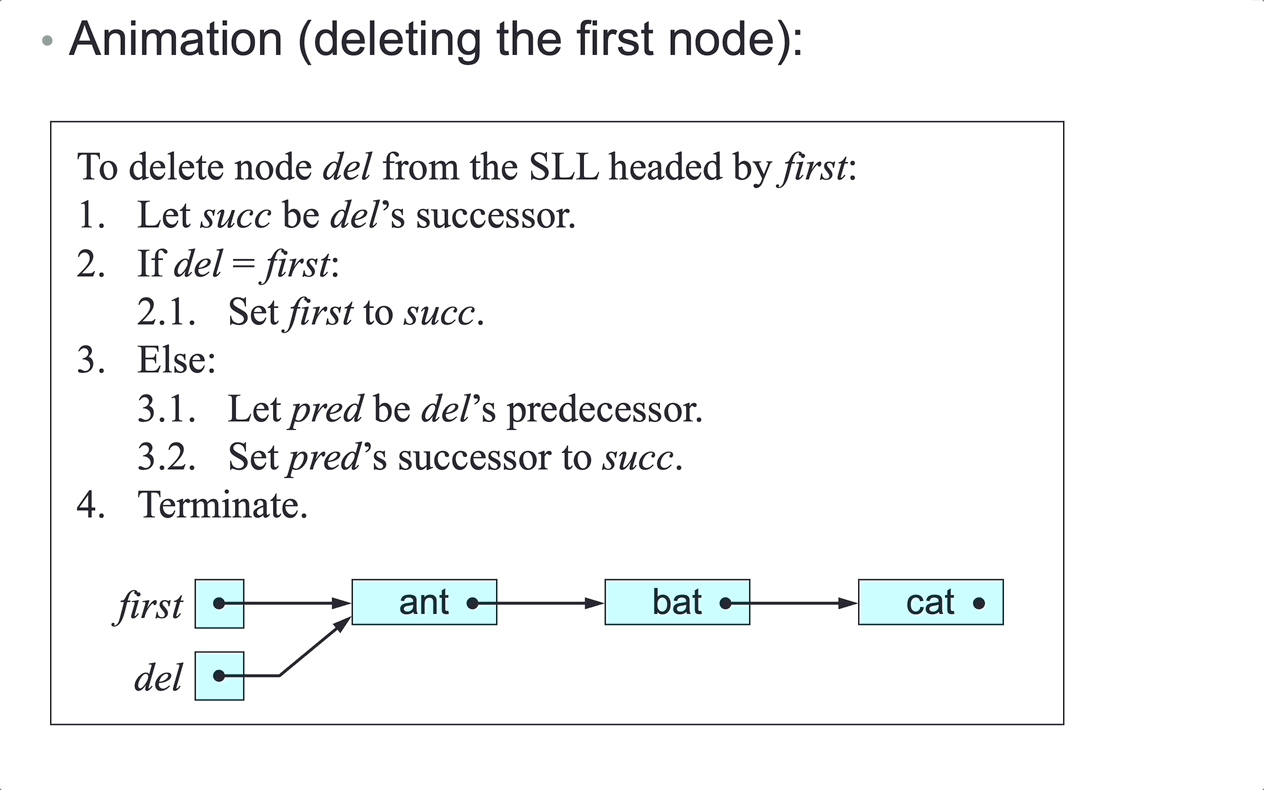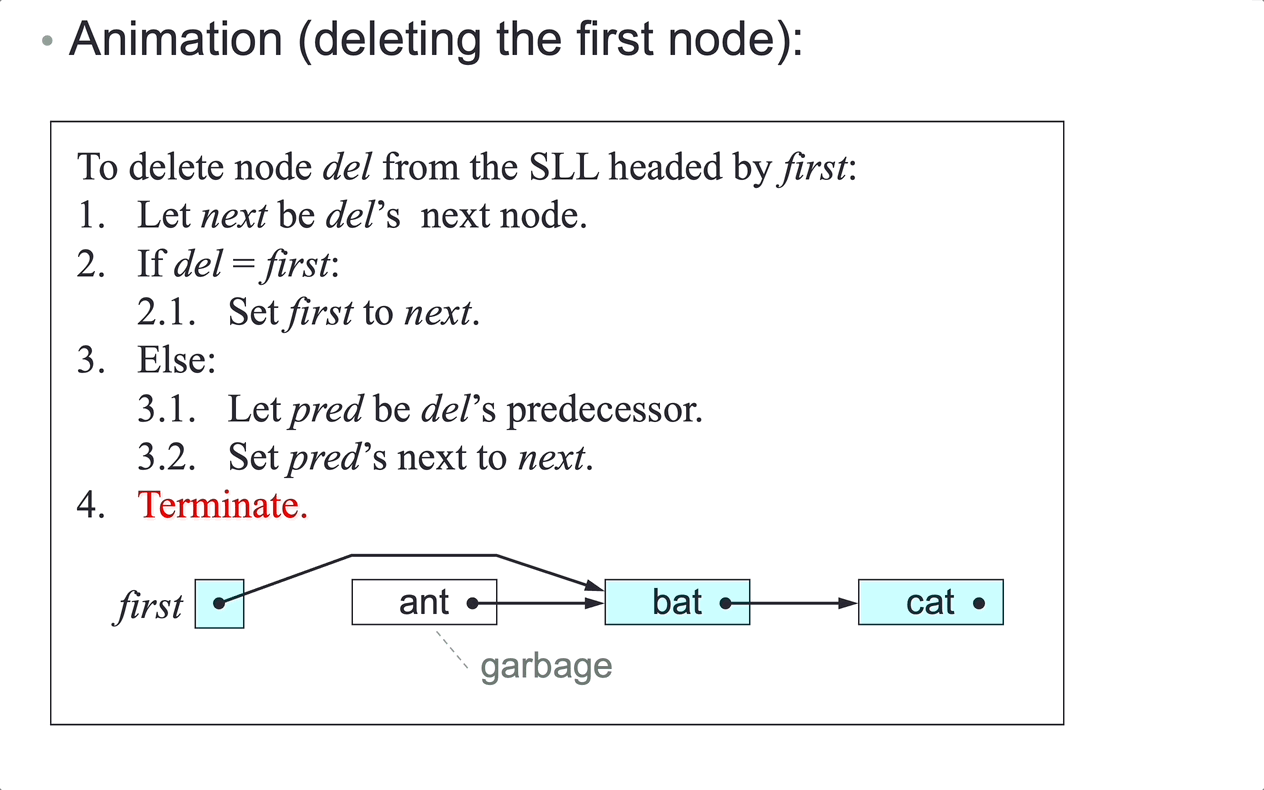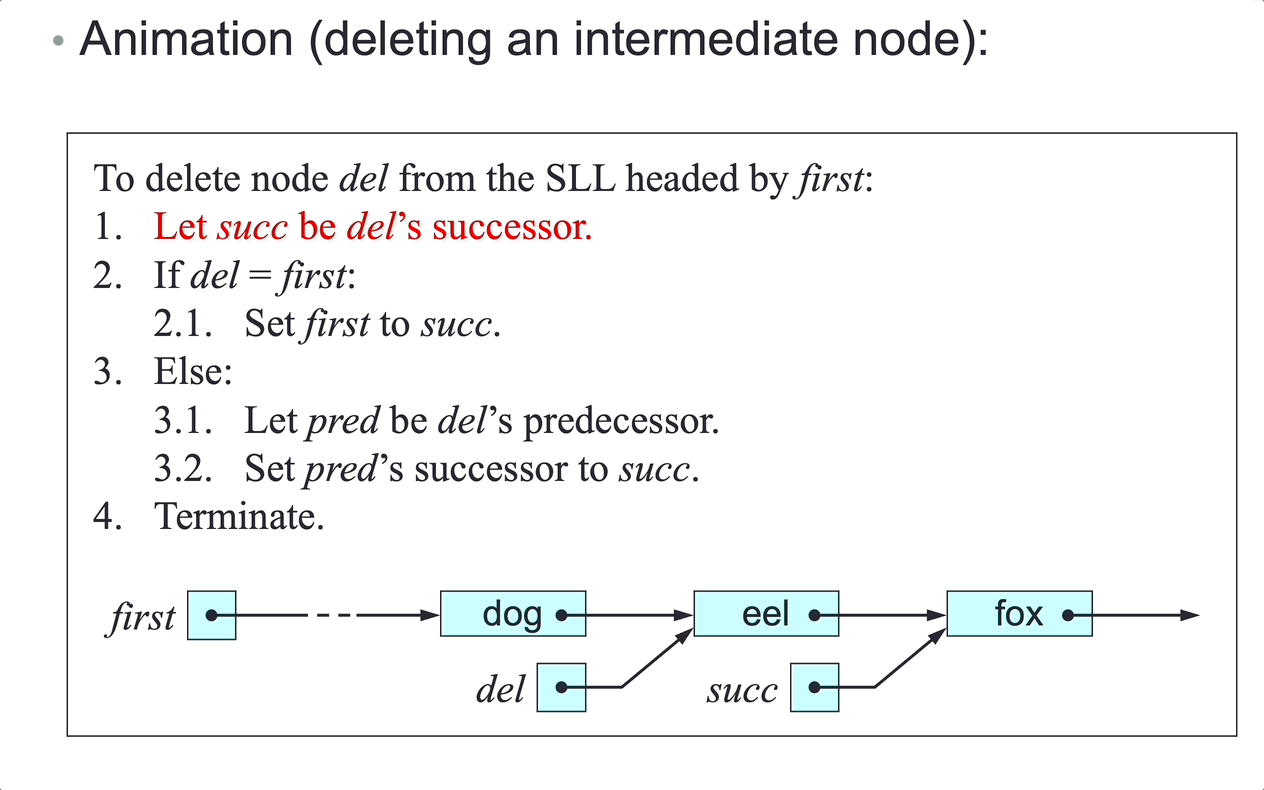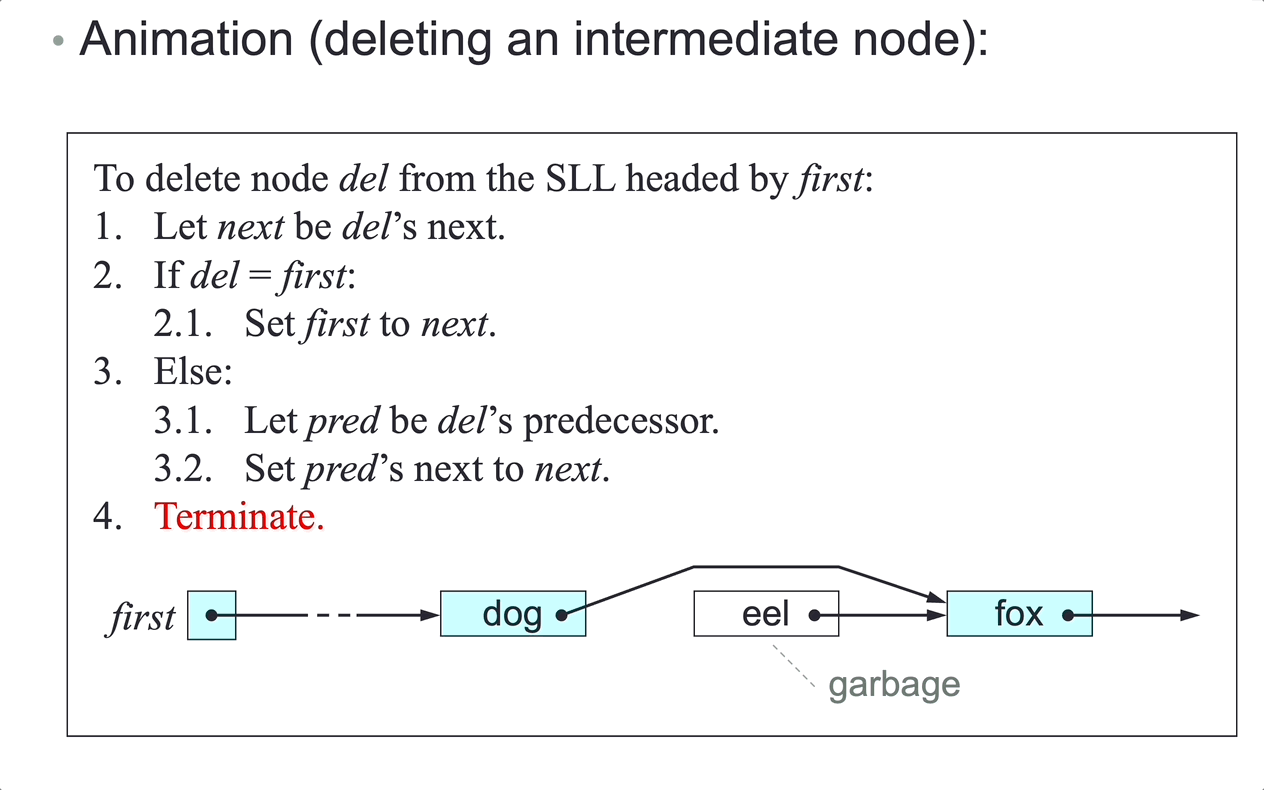
SLL deletion algorithm:

To delete node del from the SLL headed by first:

Let next be del’s next node.
if del is first, set first to next, case 1 and 2.
Else:
1. Let pred be del’s predecessor.
2. Set pred’s next to next, case 3 and 4.
Terminate.

There is no link from node del to its predecessor, so step 3.1 can access del’s predecessor only by following links from first.

Analysis:

Let n be the SLL’s length.

Step 3.1 must visit all nodes from the first node to the deleted node’s predecessor. There are between 0 and n-1 such nodes.

Average number of nodes visited is: \(\frac{n-1}{2}\).

Time complexity is O(n).

  
public void delete(Node<E> del) {
    // Delete node del from this SLL.
    Node<E> next = del.next;

    if (del == first) {
        first = next;
    } else {
        Node<E> pred = first;
        while (pred.next != del) {
            pred = pred.next;
        }
        pred.next = next;
    }
}

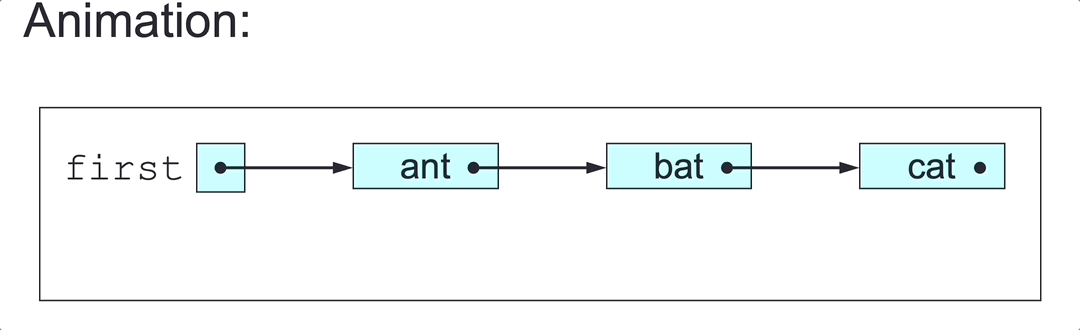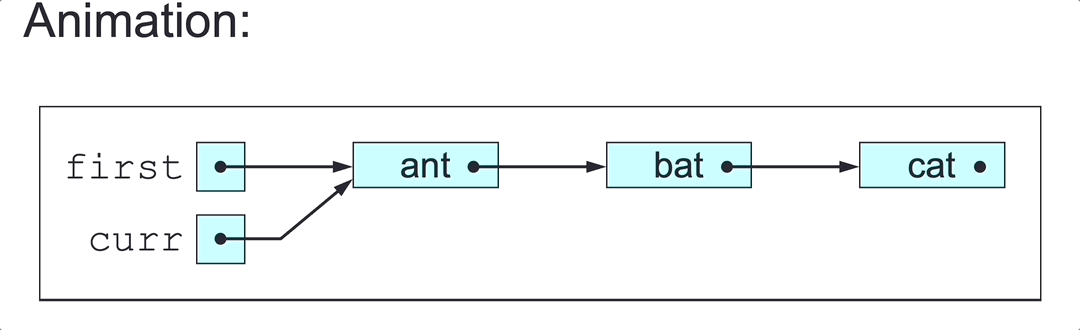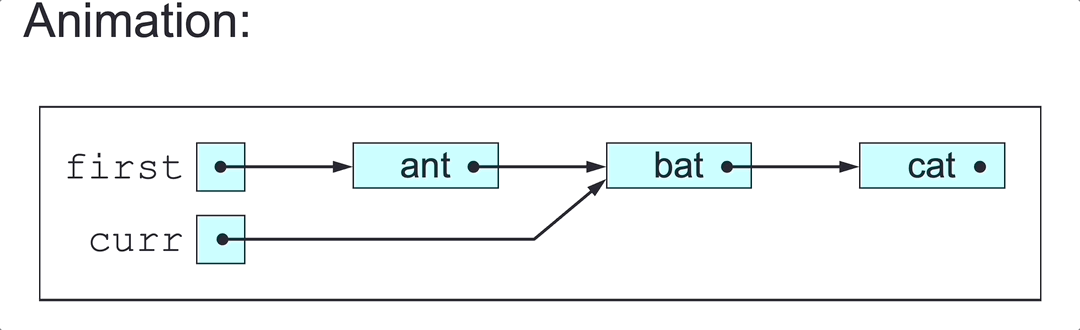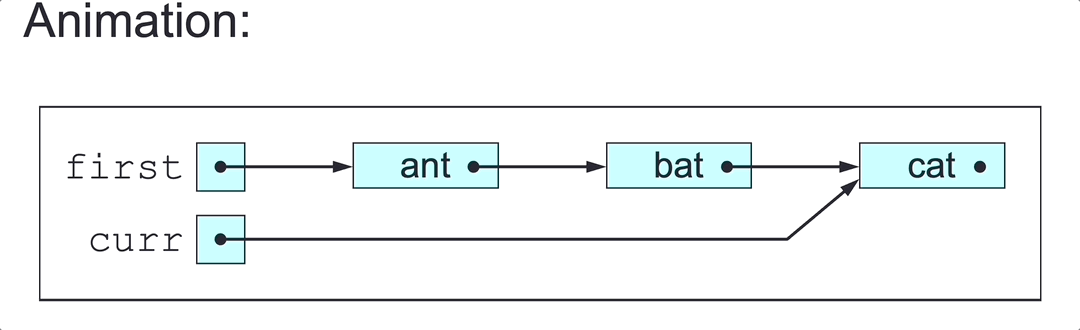
SLL Searching

Problem: search for a given target value in a linked-list.

Idea: follow links from the first node to the last node, terminating when we find a node whose element matches the target value.

Unsorted SLL linear search algorithm:

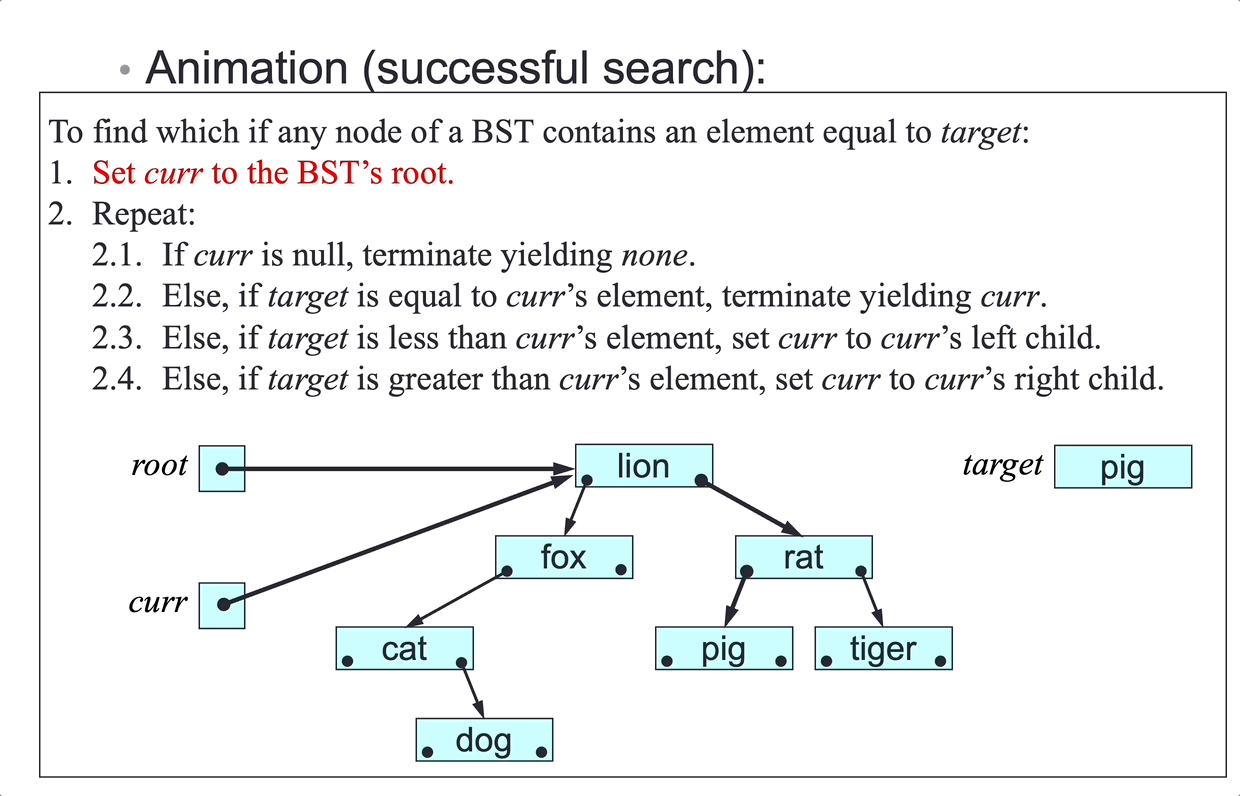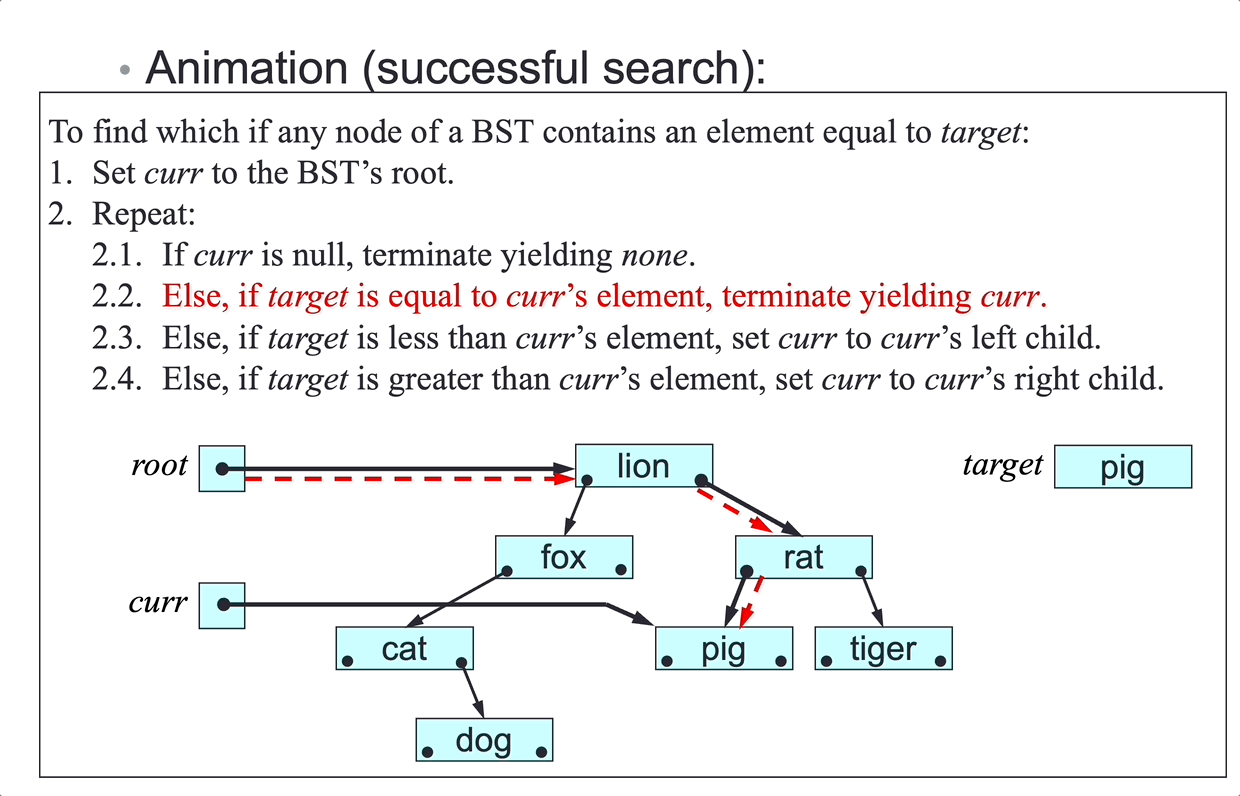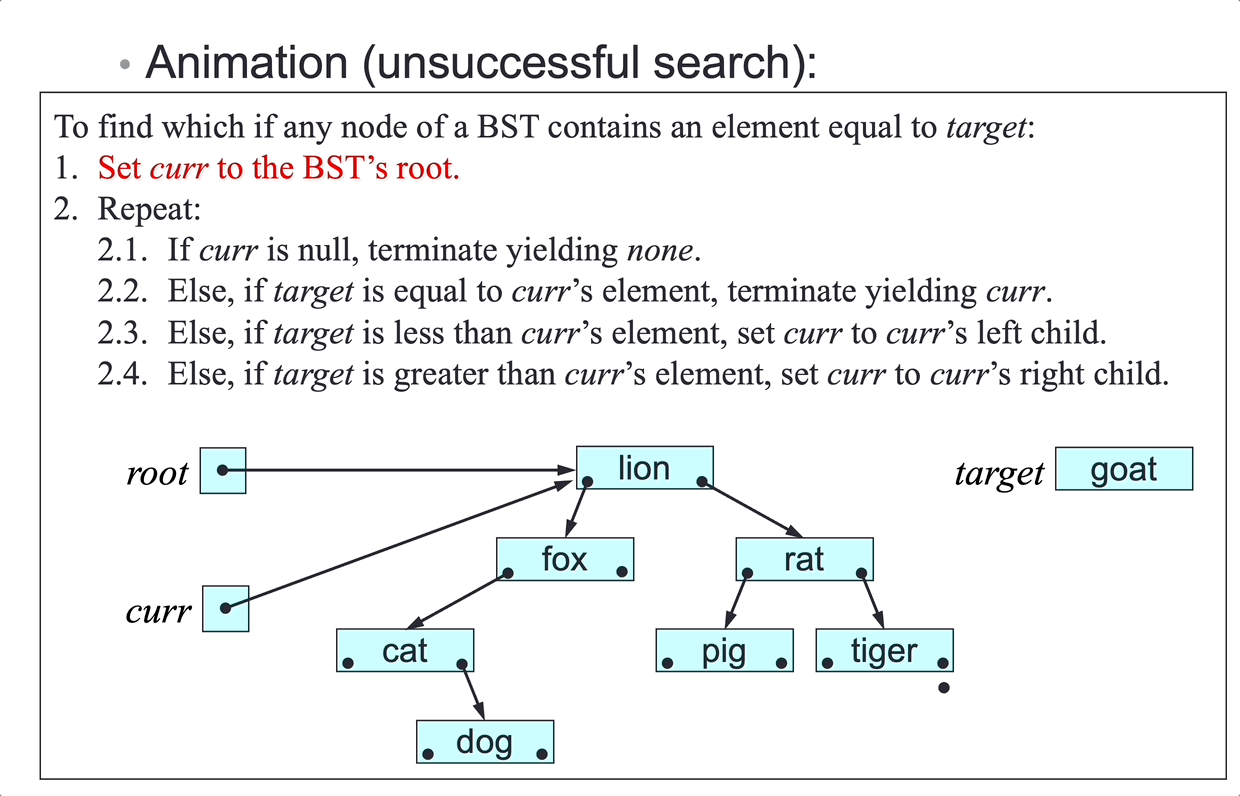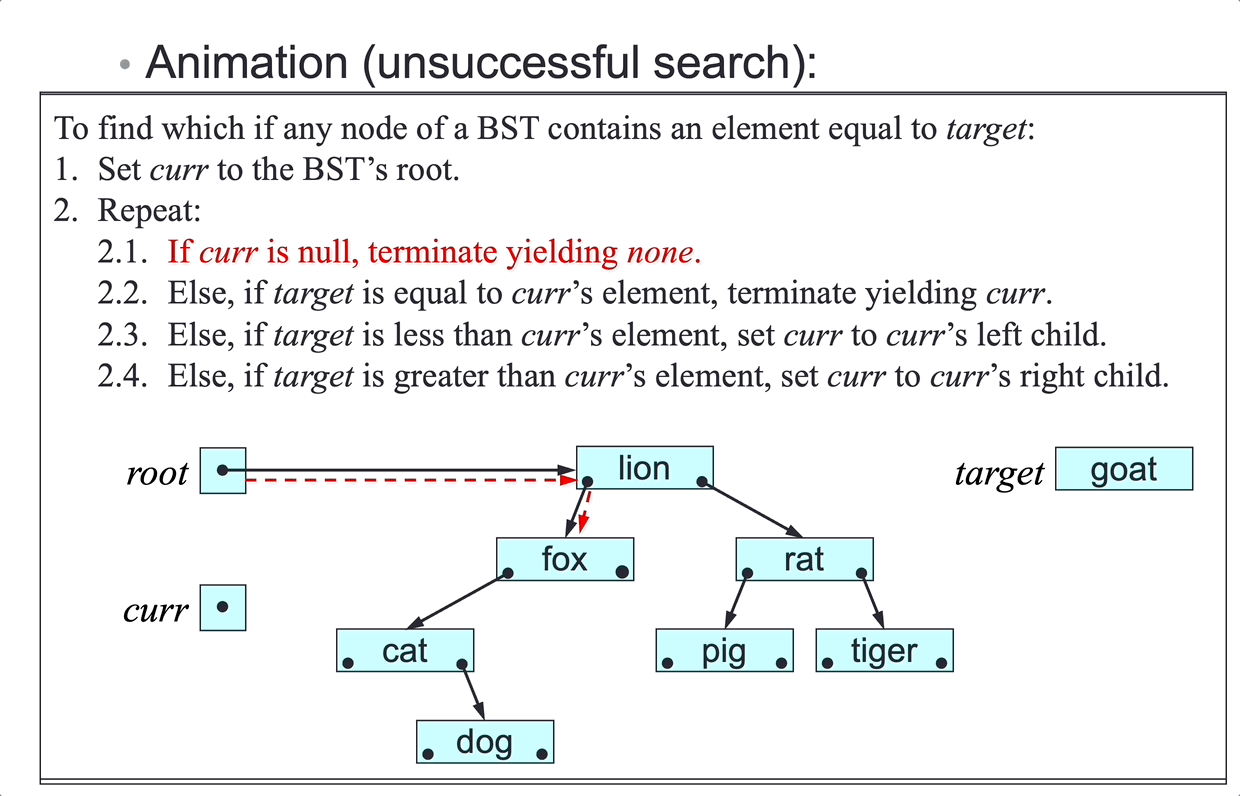
To find which (if any) node of the SLL headed by first contains an element equal to target:

For each node curr in the SLL headed by first, repeat:
1. If target is equal to curr’s element, terminate with answer curr.
Terminate yielding none.

Analysis (counting comparisons):

Let n be the SLL’s length. If the search is successful, the average number of comparisons is:

\[\frac{n+1}{2} \approx \frac{n}{2}\]

If the search is unsuccessful, the number of comparisons is \(n\).

In either case, time complexity is O(n).

  
    public Node<E> search(E target) {
        // Find which (if any) node of this SLL contains an
        // element equal to target. Return a link to the
        // matching node (or null if there is none).
        Node<E> curr = first;
        while (curr != null) {
            if (target.equals(curr.element)) return curr;
            curr = curr.next;
        }
        return null;
    }

SLL Code Example in Java

  
package linkedLists;

// generic SLL
public class SLL<E> {

    // Each SLL object is the header of
    // a singly-linked-list
    private Node<E> first;

    public SLL() {
        // Construct an empty SLL.
        first = null;
    }

    ////////// Inner class //////////
    private static class Node<E> {
        // Each Node object is a node of a
        // singly-linked-list.
        protected E element;
        protected Node<E> next;

        public Node(E elem, Node<E> n) {
            element = elem;
            next = n;
        }
    }

    public void printFirstToLast() {
        // Print all elements in this SLL, in first-to-last order.
        Node<E> curr = first;
        while (curr != null) {
            System.out.println(curr.element);
            curr = curr.next;
        }
    }

    public void insert(E elem, Node<E> pred) {
        // Insert elem at a given point in this SLL, either after the
        // node pred, or before the first node if pred is null.
        Node<E> ins = new Node<E>(elem, null);
        if (pred == null) {
            ins.next = first;
            this.first = ins;
        } else {
            ins.next = pred.next;
            pred.next = ins;
        }
    }

    public void insert(E elem) {
        // Insert elem at head of list
        insert(elem, null);
    }

    public void deleteFirst() {
        // Delete this SLLs first node (assuming length > 0).
        first = first.next;
    }

    public void delete(Node<E> del) {
        // delete node del from this SLL
        Node<E> next = del.next;
        if (del == first) first = next;
        else {
            Node<E> pred = first;
            while (pred.next != del) pred = pred.next;
            pred.next = next;
        }
    }

    public Node<E> search(E target) {
        // Find which (if any) node of this SLL contains an
        // element equal to target. Return a link to the
        // matching node (or null if there is none).
        Node<E> curr = first;
        while (curr != null) {
            if (target.equals(curr.element)) return curr;
            curr = curr.next;
        }
        return null;
    }

    public void reverse() {
        Node<E> curr = this.first;
        Node<E> pred = null;
        Node<E> next = null;
        while (curr != null) {
            next = curr.next;
            curr.next = pred;
            pred = curr;
            curr = next;
        }
        first = pred;
    }
}

Animal class to test the SLL code:

  
package linkedLists;

// simple program to test linked list classes
public class Animals {
    /**
     * @param args
     */
    public static void main(String[] args) {
        // testing the SLL
        System.out.println("Farm animals:\n ");
        SLL<String> farm = new SLL<String>();
        farm.insert("horse");
        farm.insert("cow");
        farm.insert("sheep");
        farm.insert("pig");

        farm.printFirstToLast();
        System.out.println("\n");
        farm.reverse();
        System.out.println("Reversed list is: ");
        farm.printFirstToLast();
        System.out.println("\n");
        farm.reverse();
        farm.deleteFirst();
        farm.printFirstToLast();
        System.out.println("\n");
        System.out.print("Linked list does ");
        if (farm.search("horse") == null) System.out.print("not ");
        System.out.print("contain the string \"horse\", and does ");
        if (farm.search("goat") == null) System.out.print("not ");
        System.out.print("contain the string \"goat\".");
        System.out.println("------------------------------\n");

        // testing the DLL
        System.out.println("petshop: \n");
        DLL<String> petShop = new DLL<String>();
        petShop.insert("cat");
        petShop.insert("dog");
        petShop.insert("dog");
        petShop.insert("mouse");
        petShop.printFirstToLast();
        System.out.println("\n");
        petShop.delete("dog");
        petShop.printFirstToLast();
        System.out.println("------------------------------\n");
    }
}

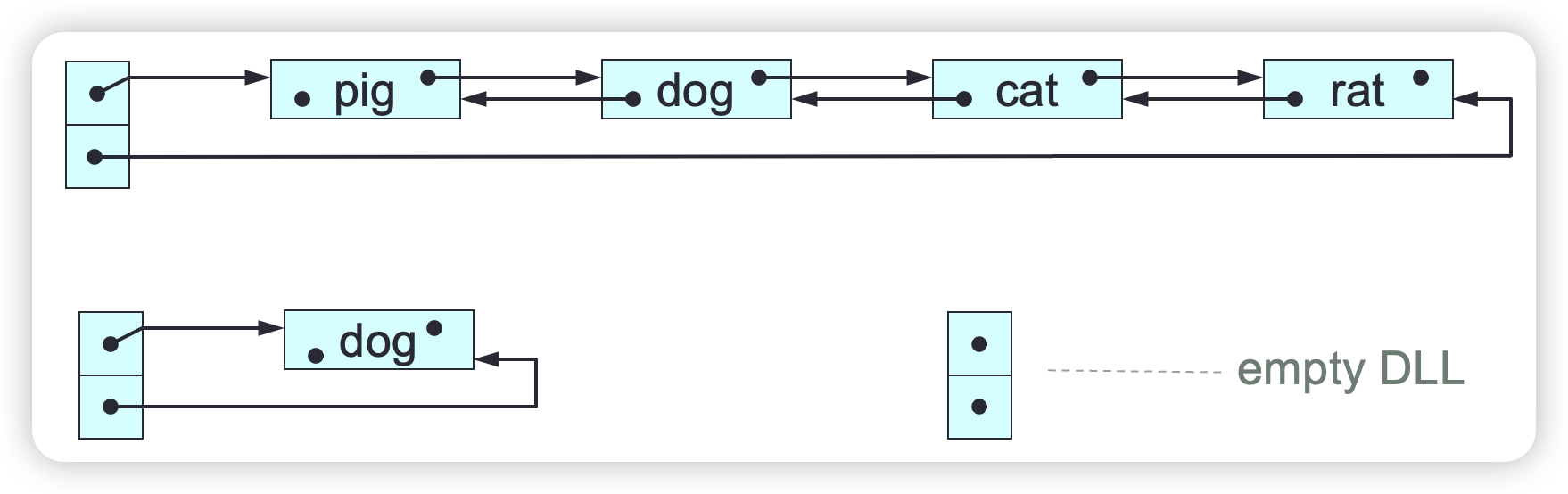
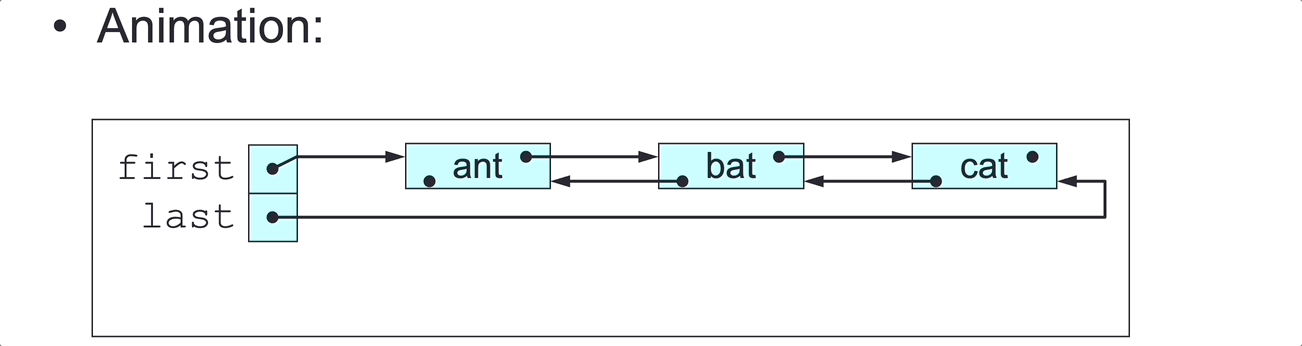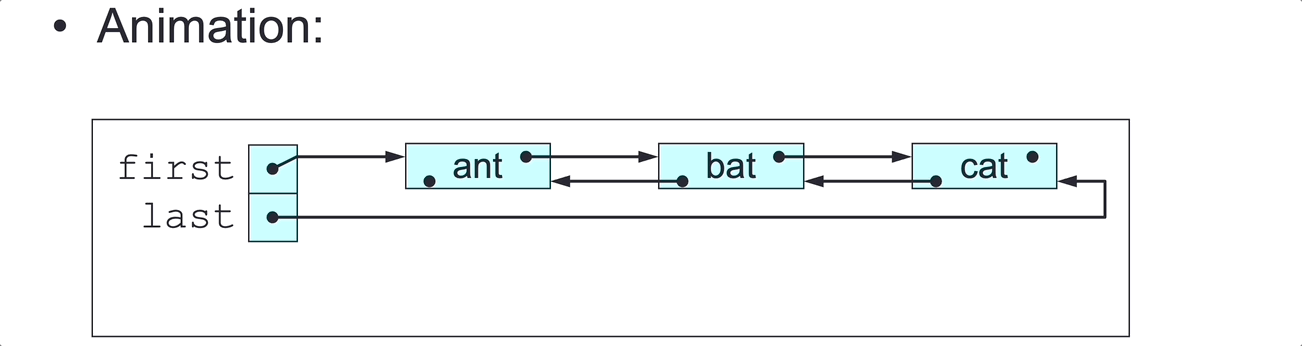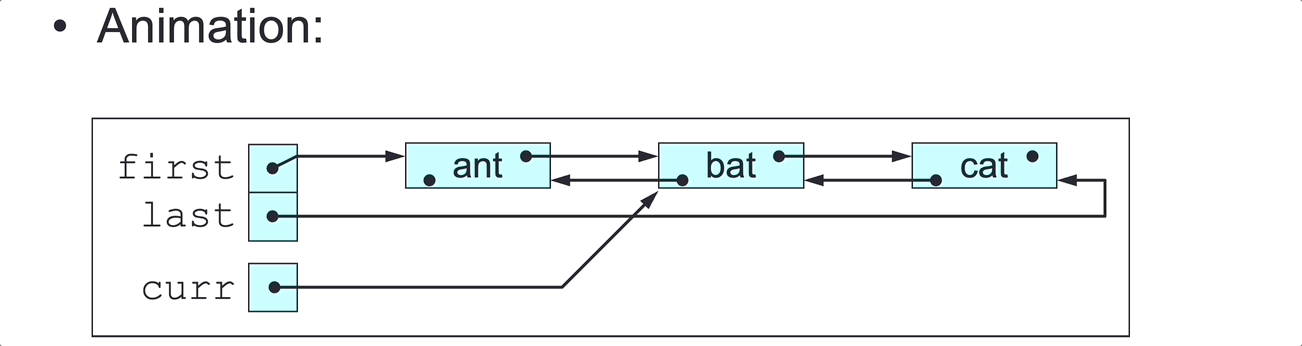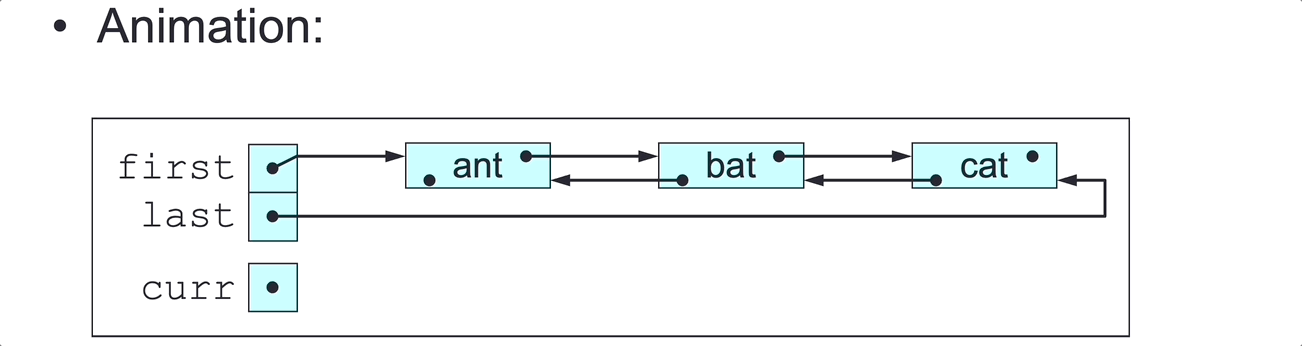
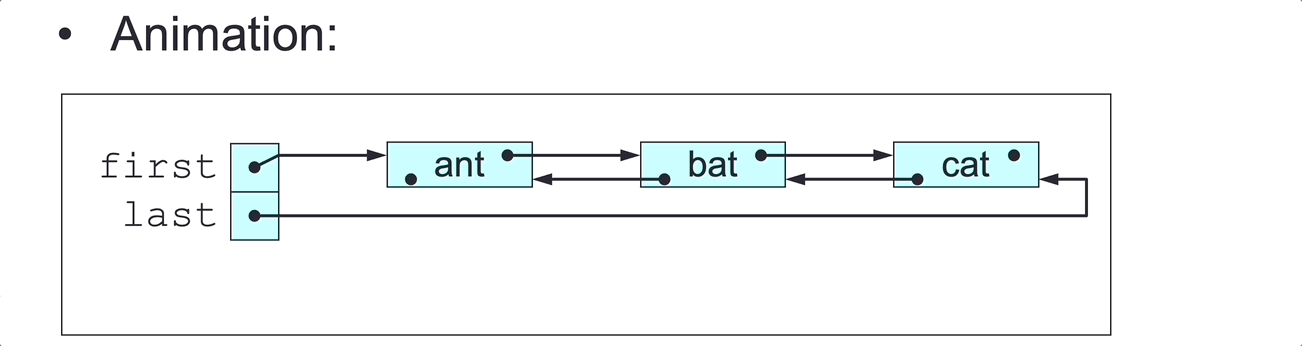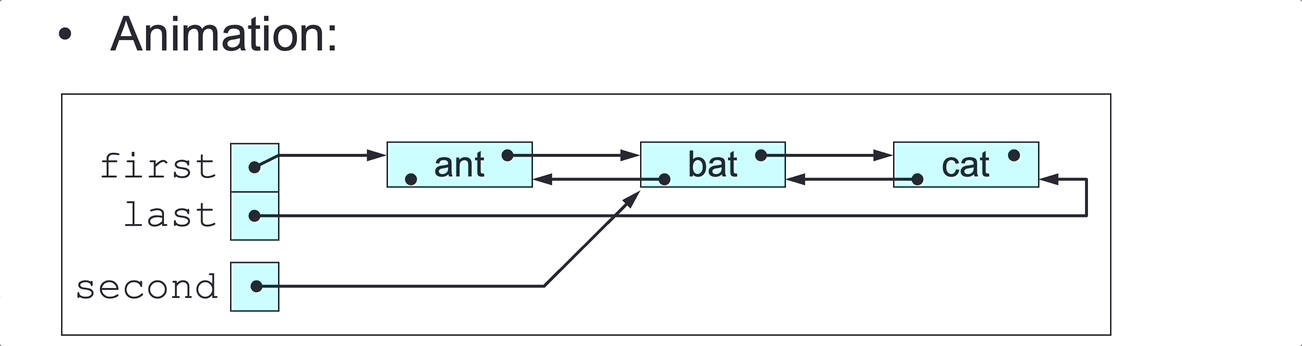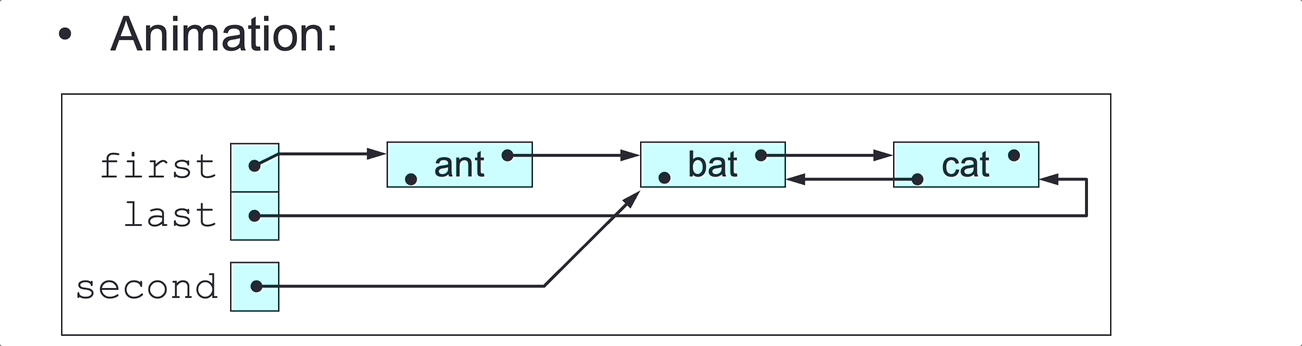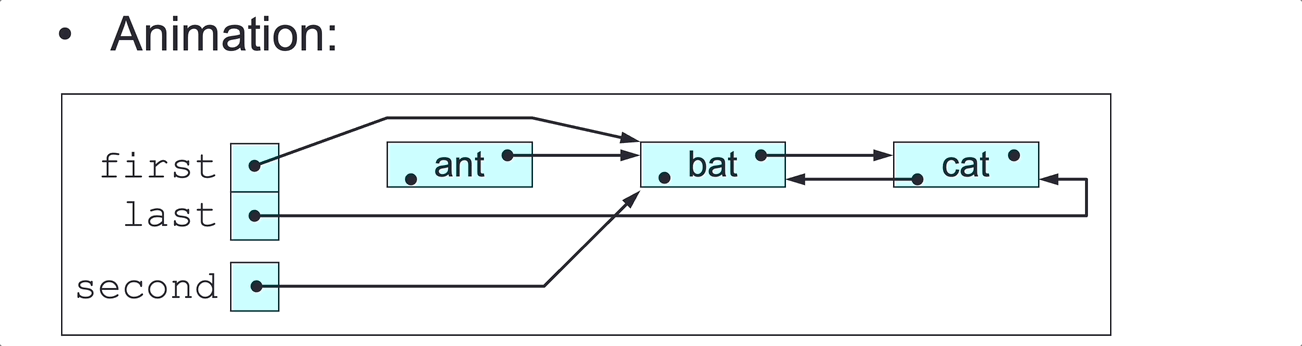
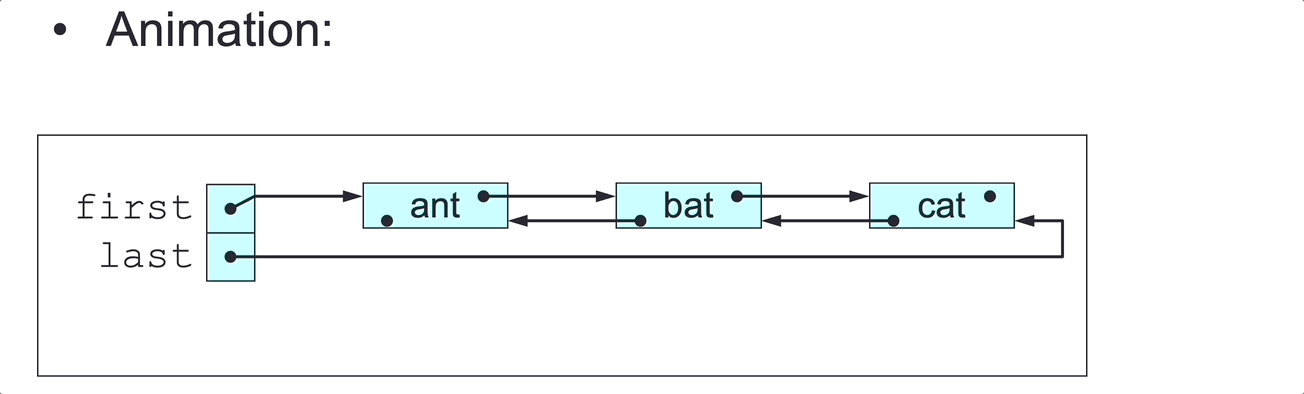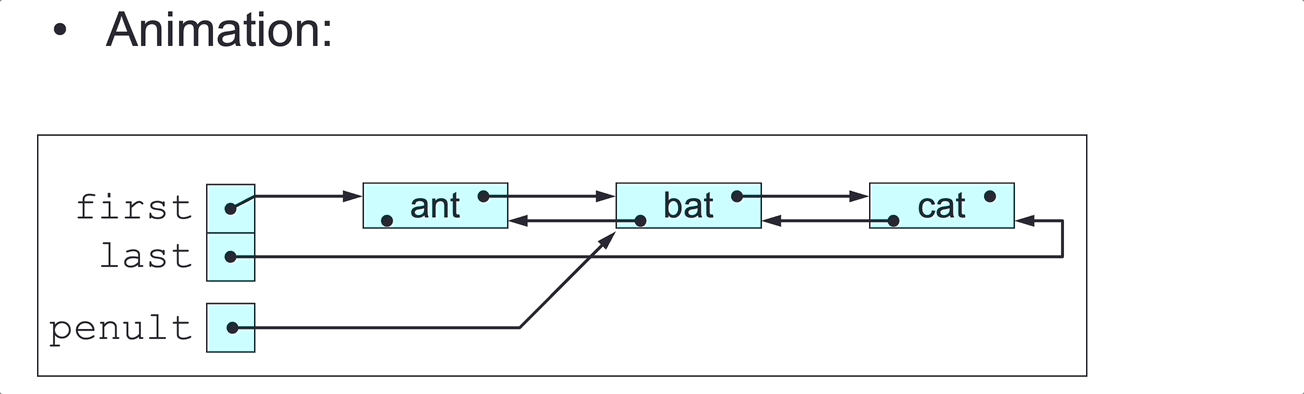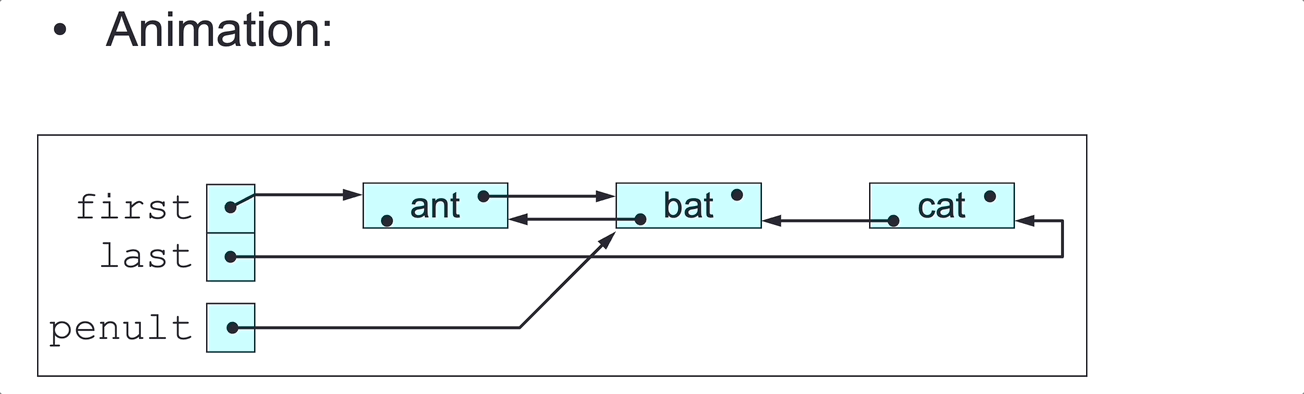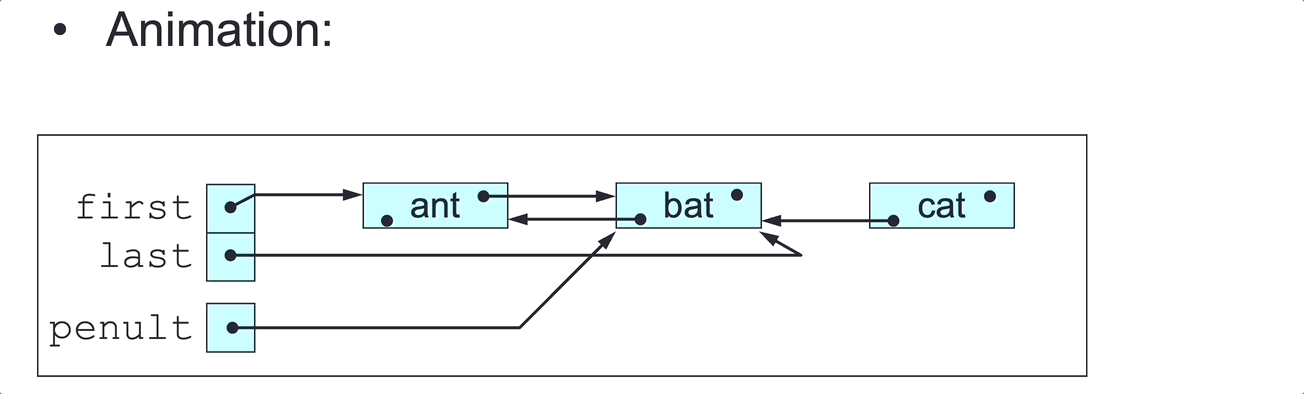
Doubly Linked Lists

A doubly linked list (DLL) consists of a header together with a sequence of nodes connected by links in both directions.

Each DLL node contains a single element, plus a link to the node’s successor (next) or null, plus a link to the node’s predecessor or null. The DLL header contains links to the DLL’s first and last nodes or null if the DLL is empty.

DLL Traversal

  
public void printLastToFirst() {
    // Print all elements in this DLL, in last-to-first order.
    Node<E> curr = last;
    while (curr != null) {
        System.out.println(curr.element);
        curr = curr.pred;
    }
}

DLL Delete First

  
public void deleteFirst() {
    // Delete this DLL’s first node (assuming length > 0).
    Node<E> second = first.next;
    second.pred = null;
    first = second;
}

DLL Delete Last

  
public void deleteLast() {
    // Delete this DLL’s last node (assuming length > 0).
    Node<E> penult = last.pred;
    penult.next = null;
    last = penult;
}

DLL Insertion

DLL insertion algorithm:

To insert elem at a given point in the DLL headed by (first, last):

Make ins a link to a newly created node with element elem and with predecessor and next both null.
If first = last = null:
1. Set first to ins.
2. Set last to ins.
Else, if the insertion point is before node first:
1. Set ins’s next to first.
2. Set first’s predecessor to ins.
3. Set first to ins.
Else, if the insertion point is after node last:
1. Set ins’s predecessor to last.
2. Set last’s next to ins.
3. Set last to ins.
Else, if the insertion point is after the node pred and before the node next:
1. Set ins’s predecessor to pred.
2. Set ins’s next to next.
3. Set pred’s next to ins.
4. Set next’s predecessor to ins.
Terminate.

DLL Deletion

DLL deletion algorithm:

To delete node del from the DLL headed by (first, last):

Let next be del’s next, and let pred be del’s predecessor.
If del = first: set first to next.
Else, set pred’s next to next.
If del = last, set last to pred.
Else, set next’s predecessor to pred.
Terminate.

Comparison of SLL and DLL Algorithms

Operation	Singly Linked List (SLL)	Doubly Linked List (DLL)
Insertion	O(1)	O(1)
Deletion	O(n)	O(1)
Search	O(n)	O(n)

DLL Code Example in Java

  
package linkedLists;

public class DLL<E> {
    // Each DLL object is the header of a
    // doubly-linked-list
    private Node<E> first, last;

    public DLL() {
        // Construct an empty DLL.
        first = null;
        last = null;
    }

    // //////// Inner class //////////
    private static class Node<E> {
        // Each DLL.Node object is a node of a
        // doubly-linked-list.
        protected E element;
        protected Node<E> pred, next;

        public Node(E elem, Node<E> pred1, Node<E> next1) {
            element = elem;
            pred = pred1;
            next = next1;
        }
    }

    public void printLastToFirst() {
        // Print all elements in this DLL, in last-to-first order.
        Node<E> curr = last;
        while (curr != null) {
            System.out.println(curr.element);
            curr = curr.pred;
        }
    }

    public void deleteFirst() {
        // delete the DLL's first node (assuming length>0)
        Node<E> second = first.next;
        second.pred = null;
        first = second;
    }

    public void deleteLast() {
        // delete the DLL's last node (assuming length>0)
        Node<E> penult = last.pred;
        penult.next = null;
        last = penult;
    }

    public void delete(Node<E> del) {
        Node<E> next = del.next;
        Node<E> pred = del.pred;
        if (del == first) first = next;
        else {
            pred.next = next;
            if (del == last) last = pred;
            else next.pred = pred;
        }
    }

    // delete any node containing this value
    public void delete(E elem) {
        if (first != null) {
            Node<E> p = first;
            while (p != null) {
                if (p.element.equals(elem)) {
                    this.delete(p);
                    p = first;
                } else p = p.next;
            }
        }
    }

    public void insert(E elem, Node<E> pred) {
        // Insert elem at a given point in this SLL, either after the
        // node pred, or before the first node if pred is null.
        Node<E> ins = new Node<E>(elem, null, null);
        if (first == null && last == null) { // list is empty
            first = ins;
            last = ins;
        } else {
            if (pred == null) { // inserting at head
                ins.next = first;
                first.pred = ins;
                first = ins;
            } else { // inserting after last node
                if (pred == last) {
                    ins.pred = last;
                    last.next = ins;
                    last = ins;
                } else {
                    DLL.Node<E> next = pred.next;
                    ins.pred = pred;
                    ins.next = next;
                    pred.next = ins;
                    next.pred = ins;
                }
            }
        }
    }

    public void insert(E elem) {
        insert(elem, null);
    }

    public void printFirstToLast() {
        // Print all elements in this DLL, in first-to-last order.
        Node<E> curr = first;
        while (curr != null) {
            System.out.println(curr.element);
            curr = curr.next;
        }
    }
}

Week 5: Abstract Data Types and Collections

Data types and abstract data types (ADTs)
Requirements, contracts, implementations of ADTs
Design of ADTs in Java
Collections
Abstract data types in the Java class library

Data Types

We classify all data into data types. Each data type is characterized by:

a set of values
a data representation common to all these values
a set of operations which can be applied uniformly to these values

For example, boolean is a built-in data type in Java, the values are false and true. The data representation is a single byte, 00000000 = false, 00000001 = true. The operations are &&, ||, !, etc.

To introduce a new data type, we must define its values, its data representation, and its operations. In java, we use a class declaration. The class’s instance variables determine the values and data representation. The class’s constructors and methods are the operations.

Example: Date data type

Could represent a Date in several ways, using 3 integers to represent y, m and d, say, or a single integer to represent the day-in-epoch where 0 represents 1 in Jan 2000.

Good program practice: application code should NOT

admit improper values, an exception should be thrown
access the data representation, i.e. should use information hiding, keep instance variables private, use Getters and Setters.
be aware of the data representation, we should be able to change the representation and not affect application code

Abstract Data Types

An abstract data type (ADT) is characterized by:

a set of values
a set of operations

However it’s not characterized by its data representation.

The data representation is private, so application code cannot access it. Only the ADT’s operations can access it. The data representation can be changed, with no effect on application code. Only the ADT’s operations must be recoded.

ADT Specification

Each ADT should have a contract that:

specifies the set of values of the ADT
specifies each operation of the ADT, its name, parameter, type, result type, observable behavior.
the contract does not specify the data representation, nor how the operations are implemented.
the observable behavior of an operation is its effect as observed by the application code. For example, an observable behavior can be sorting an array, and the algorithm with that behavior is quick sort.

Separation of concerns:

The ADT programmer undertakes to provide an implementation of the ADT that respects the contract. This programmer is not concerned with what application the ADT is used for.

The application programmer undertakes to process values of the ADT using only the operations specified in the contract. This programmer is not concerned with how the ADT is implemented.

An implementation of an ADT entails:

deciding a data representation: choosing a data structure
implementing each operation: choosing an algorithm

The data representation must be private, and cover all proper values. If the data representation also admits improper values, the operations must avoid generating them. The algorithms must be consistent with the data representation.

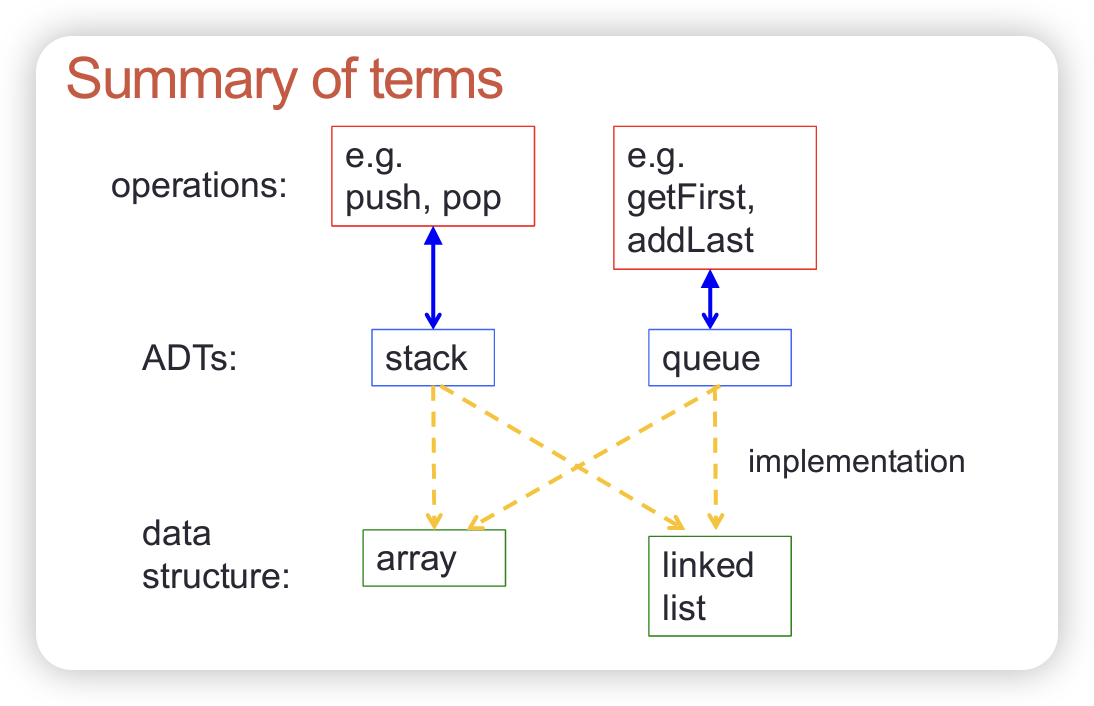
Collections

A collection is a group of elements.

For example:

stack
queue
list
set
map

A collection is empty if it contains no elements. The size of a collection is the number of elements it contains. A collection is bounded if its size is capped. A collection is heterogeneous if its elements may be of different types. A collection is homogeneous if its elements are all of the same type.

In Java, a heterogeneous collection is implemented by an ordinary class, with elements of type Object. A homogeneous collection is implemented by a generic class, with elements of type E where E is the generic class’s type parameter or possibly elements consisting of multiple types like Pair<K,V>, but all elements have the same multiple type.

Code Examples in Java

  
package adts;

public class Date {
    public static final int[] LAST = {31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};
    // Each Date object is a past, present, or future date.
    // This date is represented by a day-in-epoch
    // number d (where 0 represents 1 January 2000):
    public int y, m, d;

    public Date(int y, int m, int d) throws InvalidDateException {
        if (m < 1 || d > LAST[m])
            throw new InvalidDateException(d + "," + m + "," + y); // improper date
        this.y = y;
        this.m = m;
        this.d = d;
    }

    public void advance(int n) {
        int y = this.y, m = this.m, d = this.d + n;

        while (d > LAST[m]) {
            d -= LAST[m];
            if (m < 12) m++;
            else {
                m = 1;
                y++;
            }
        }

        this.y = y;
        this.m = m;
        this.d = d;
    }

    @Override
    public String toString() {
        return ("(" + d + "," + m + "," + y + ")");
    }

    public static void main(String[] args) throws InvalidDateException {
        Date d1 = new Date(2009, 4, 28);
        d1.advance(40);
        System.out.println("The new date is " + d1);
    }
}

public class InvalidDateException extends Exception {
    /** */
    private static final long serialVersionUID = 1L;

    private String badDate;

    // constructor
    public InvalidDateException(String bd) {
        super(bd); // constructor for superclass
    }

    public String getBadDate() {
        return badDate;
    }

    public void setBadDate(String bd) {
        badDate = bd;
    }
}

  
package adts;

// the purpose of this example is to show how a String Interface might be defined
// we have to call it something different to avoid confusion with the actual String class
// otherwise it's just a String (all strings are actually immutable!)
public interface ImmutableString {

    public int length();

    // Return the length of this string.

    public char charAt(int p);

    // Return the character at position p in this string.

    public boolean equals(ImmutableString that);

    // Return true if and only if this string is equal to that.

    public int compareTo(ImmutableString that);

    // Return -1 if this string is lexicographically less than
    // that, or 0 if this string is equal to that,
    // or +1 if this string is lexicographically greater than that.

    public ImmutableString subString(int i1, int i2);

    // return the substring between indices i1 and i2-1

    /////////////// Transformer ///////////////
    public ImmutableString concat(
            ImmutableString
                    that); // Return the string obtained by 	// concatenating this string and that.
}

  
package adts;

public interface Pair<E> {
    // Each Pair<E> object is a homogeneous Pair whose elements are of type E.

    /////////////// Accessors ///////////////
    public E first(); // Return first element of a pair

    public E second(); // Return seond element

    ////////////// Transformers //////////////
    public void updateFirst(E e1); // replace first element with e1

    public void updateSecond(E e2); // replace first element with e1
}

public class Pair1<E> implements Pair<E> {

    private E first;
    private E second;

    public Pair1(E f, E s) {
        first = f;
        second = s;
    }

    @Override
    public E first() {
        return first;
    }

    @Override
    public E second() {
        return second;
    }

    @Override
    public void updateFirst(E e1) {
        first = e1;
    }

    @Override
    public void updateSecond(E e2) {
        second = e2;
    }
}

public class Pair2<E extends Comparable<E>> implements Pair<E>, Comparable<Pair2<E>> {

    private E first;
    private E second;

    public Pair2(E e1, E e2) {
        first = e1;
        second = e2;
    }

    @Override
    public E first() {
        return first;
    }

    @Override
    public E second() {
        // TODO Auto-generated method stub
        return second;
    }

    @Override
    public void updateFirst(E e1) {
        first = e1;
    }

    @Override
    public void updateSecond(E e2) {
        second = e2;
    }

    public String toString() {
        return "[" + first + "," + second + "]";
    }

    @Override
    public int compareTo(Pair2<E> e) {
        if (first.compareTo(e.first) > 1
                || (first.compareTo(e.first) == 0 && second.compareTo(e.second) > 0)) return 1;
        if (first.compareTo(e.first) == 0 && second.compareTo(e.second) == 0) return 0;
        return -1;
    }
}

public class TestPair {

    /**
     * @param args
     */
    public static void main(String[] args) {
        Pair1<String> me = new Pair1<>("Alice", "Miller");
        String my_name = me.first();
        System.out.println("my name is " + my_name);
        Person pierre = new Person("Pierre", "Curie");
        Person marie = new Person("Marie", "Curie");
        Pair1<Person> curies = new Pair1<>(pierre, marie);
        Person p = curies.second();
        System.out.println("The most famous Curie is " + p);

        // to demonstrate the difference with Pair2 - can do a comparison
        // ok to use E as Integer here, as ints are comparable

        Pair2<Integer> newIntPair1 = new Pair2<>(3, 5);
        Pair2<Integer> newIntPair2 = new Pair2<>(1, 7);

        System.out.println("The pairs are: " + newIntPair1 + " and " + newIntPair2);
        System.out.print("\nThe first pair is ");
        int val = newIntPair1.compareTo(newIntPair2);
        if (val > 0) System.out.print("greater than ");
        if (val < 0) System.out.print("smaller than ");
        if (val == 0) System.out.print("the same as  ");
        System.out.print("\nThe second pair ");
    }
}

Week 6: Stacks

Overview

Stack concepts
Stack applications
Stack ADTs: requirements, contracts
Implementation of stacks: using arrays and linked-lists
Stacks in the Java class library

Stack concepts

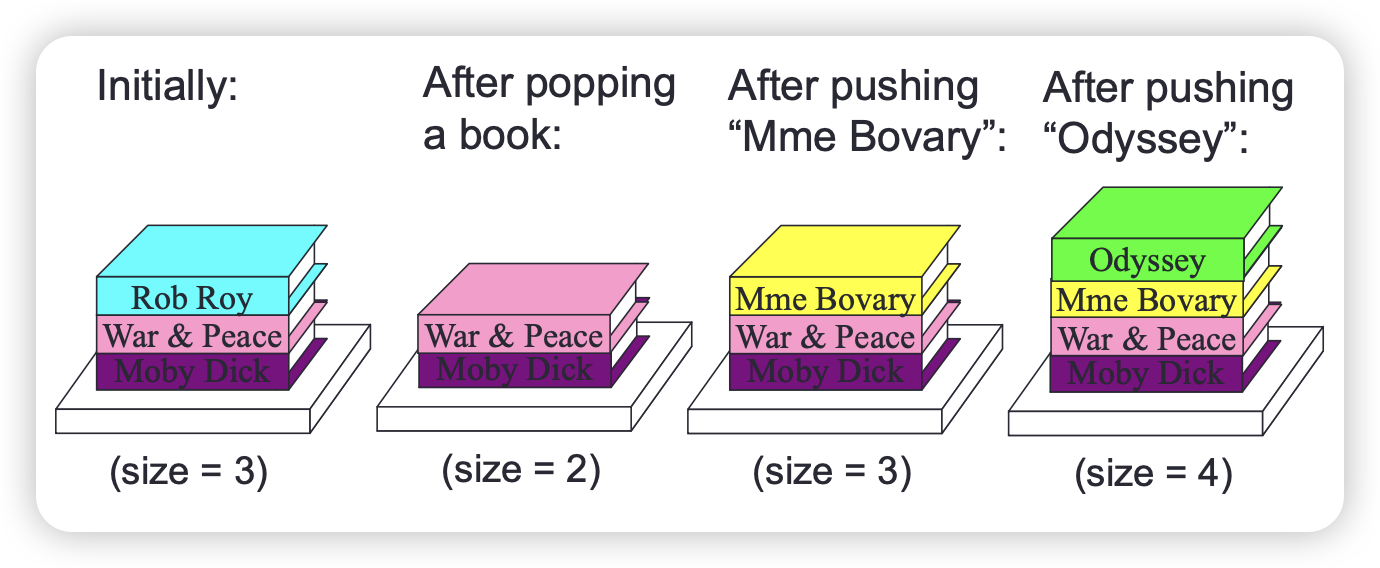
A stack is a last-in-first-out sequence of elements. Elements can be added and removed only at one end (the top of the stack). We can push an element on to the stack, i.e., add it at the top of the stack. We can pop an element from the stack, i.e., remove it from the top of the stack. The size (or depth) of a stack is the number of elements it contains.

Consider a stack of books on a table:

It is a stack because we can add(push) and remove(pop) books only at the top.

Stack Applications

Interpreter (e.g., Java Virtual Machine):

uses a stack to contain intermediate results during evaluation of complicated expressions
also uses the stack to contain arguments and return addresses for method calls and returns.

Parser (e.g., XML parser, parser in Java compiler):

uses a stack to contain symbols encountered during parsing of the source code.

Example: text-file reversal

A text file is a sequence of zero or more lines. To reverse the order of these lines, we must store them in a first-in-last-out sequence.

Text-file reversal algorithm:

To make file output contain the lines of file input in reverse order:

Make line-stack empty.
For each line read from input, repeat: push line on line-stack.
While line-stack is not empty, repeat:
1. Pop a line from line-stack into line.
2. Write line to output.
Terminate.

  
package stacks;

import java.io.BufferedReader;
import java.io.BufferedWriter;
import java.io.FileReader;
import java.io.FileWriter;
import java.io.IOException;

public class FileReversal {

    /**
     * @param args
     */
    public static void reverse(BufferedReader input, BufferedWriter output) throws IOException {
        // Make output contain the lines of input in reverse
        // order.
        Stack<String> lineStack = new ArrayStack<String>(100);

        for (; ; ) {
            String line = input.readLine();
            if (line == null) break; // end of input
            lineStack.push(line);
        }
        input.close();
        while (!lineStack.isEmpty()) {
            String line = lineStack.pop();
            output.write(line + "\n");
        }
        output.close();
    }

    public static void main(String[] args) throws IOException {
        BufferedReader input = new BufferedReader(new FileReader("reverseTestFile.txt"));
        BufferedWriter output = new BufferedWriter(new FileWriter("outputFile"));
        reverse(input, output);
        input.close();
        output.close();
    }
}

Example: bracket matching

A phrase is well-bracketed if:

for every left bracket, there is a later matching right bracket.
for every right bracket, there is an earlier matching left bracket.
the sub-phrase between a pair of matching brackets is itself well-bracketed.

Bracket matching algorithm:

To test whether phrase is well-bracketed:

Make bracket-stack empty.
For each symbol sym in phrase, scanning from left to right, repeat:
1. If sym is a left bracket: push sym on bracket-stack
2. Else, if sym is a right bracket:
  1. If bracket-stack is empty, terminate with false
  2. Pop a bracket from bracket-stack into left.
  3. If left and sym are not matched brackets, terminate with false
Terminate with true if bracket-stack is empty, or with false otherwise.

Stack ADT: requirements

it must be possible to make a stack empty.
it must be possible to push an element onto a stack.
it must be possible to pop the topmost element from a stack.
it must be possible to test whether a stack is empty.
it should be possible to access the topmost element in a stack without popping it.

Stack ADT: contract

Possible contract for homogeneous stacks:

  
public interface Stack<E> {
    // Each Stack<E> object is a homogeneous stack whose elements are of type E.
    /////////////// Accessors ///////////////
    public boolean isEmpty(); // Return true if and only if this stack is empty.

    public E peek(); // Return the element at the top of this stack.

    ////////////// Transformers ///////////////
    public void clear(); // Make this stack empty.

    public void push(E it); // Add it as the top element of this stack.

    public E pop(); // Remove and return the element at the top of this stack.
}

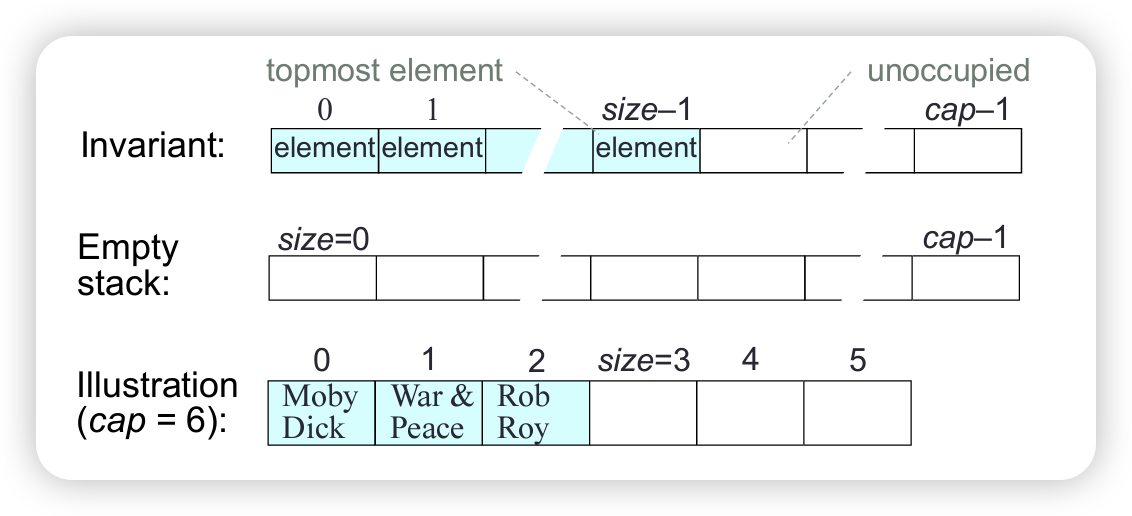
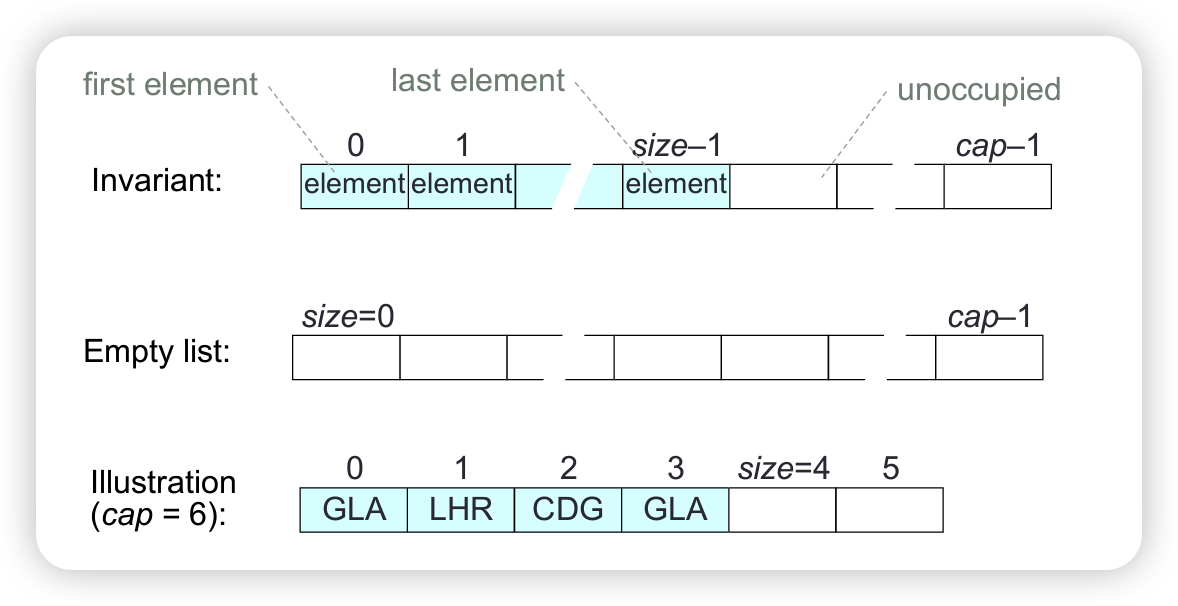
Implementation of Stacks Using Arrays

Represent a bounded stack, size <= cap, by:

a variable size
an array elems of length cap, containing the elements in elems[0...size-1]

  
package stacks;

import java.util.NoSuchElementException;

public class ArrayStack<E> implements Stack<E> {

    /**
     * @param args
     */
    private E[] elems;

    private int size;

    //// Constructor ///
    @SuppressWarnings("unchecked")
    public ArrayStack(int cap) {
        elems = (E[]) new Object[cap];
        size = 0;
    }

    /////////////// Accessors ///////////////

    @Override
    public boolean isEmpty() {
        return (size == 0);
    }

    @Override
    public E peek() {
        if (size == 0) throw new NoSuchElementException("Can't peek empty stack");
        return elems[size - 1];
    }

    ////////////// Transformers ///////////////
    @Override
    public void clear() {
        size = 0;
    }

    @Override
    public void push(E it) {
        if (size == elems.length)
            throw new ArrayIndexOutOfBoundsException("Can't push to a full stack");
        elems[size++] = it;
    }

    @Override
    public E pop() {
        if (size == 0) throw new NoSuchElementException("Can't pop from empty stack");
        ;
        E topElem = elems[--size];
        elems[size] = null;
        return topElem;
    }
}

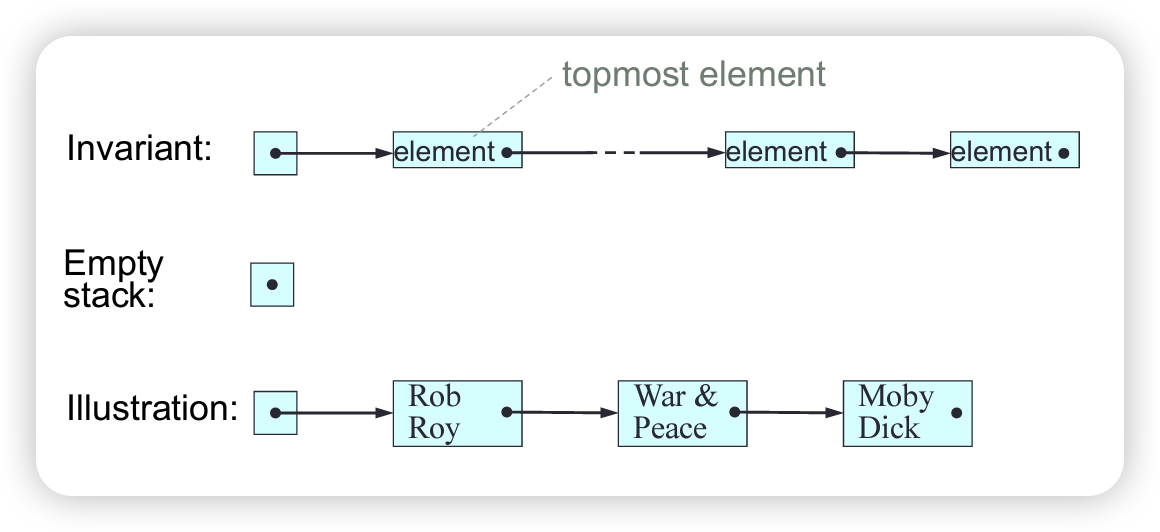
Implementation of Stacks Using SLL

Represent an unbounded stack by an SLL, such that the first node contains the topmost element.

  
package stacks;

import java.util.NoSuchElementException;

public class LinkedStack<E> implements Stack<E> {
    private Node<E> top;

    /////////////// Inner class ///////////////
    private static class Node<E> {
        public E element;
        public Node<E> next;

        public Node(E x, Node<E> n) {
            element = x;
            next = n;
        }
    }

    /////////////// Constructor ///////////////
    public LinkedStack() {
        top = null;
    }

    /////////////// Accessors ///////////////
    @Override
    public boolean isEmpty() {
        return (top == null);
    }

    @Override
    public E peek() {
        if (top == null) throw new NoSuchElementException("Can't peek empty stack");
        return top.element;
    }

    ////////////// Transformers ///////////////
    @Override
    public void clear() {
        top = null;
    }

    @Override
    public void push(E it) {
        Node<E> temp = new Node<E>(it, top);
        top = temp;
    }

    @Override
    public E pop() {
        if (top == null) throw new NoSuchElementException("Can't peek empty stack");
        E topElem = top.element;
        top = top.next;
        return topElem;
    }
}

Week 7: Queues

Queue concepts
Queue applications
A queue ADT: requirements, contract
Implementations of queues: using arrays and linked-lists
Queues in the Java class library

Queue concepts

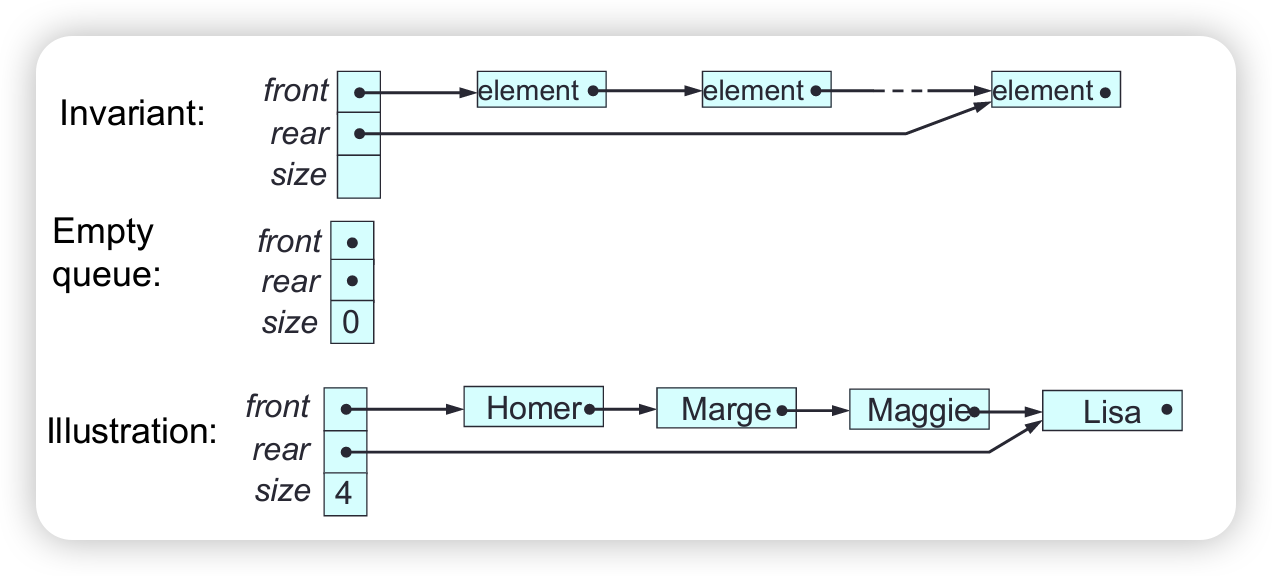
A queue is a first-in-first-out sequence of elements.

Elements can be added only at one end, the rear of the queue and removed only at the other end, the front of the queue. The size or length of a queue is the number of elements in contains.

Queue applications

Print server, uses a queue of print jobs.

Operating system, disk driver uses a queue of disk input/output requests. Scheduler uses a queue of processes awaiting a slice of processor time.

Example: demerging

• Consider a file of person records, each of which contains a person’s name, gender, birth-date, etc. The records are sorted by birth-date. We are required to rearrange the records such that females precede males, but they remain sorted by birth-date within each gender group.

Bad idea: use a sorting algorithm. Time complexity is O(n log n) at best.

Good idea: use a demerging algorithm. Time complexity is O(n).

demerging algorithm:

To copy a file of person records from input to output, rearranged such that females precede males, but their order is otherwise unchanged:

Make empty queues females and males.
For each person p in input, repeat:
1. If p is female, add p at the rear of females.
2. If p is male, add p at the rear of males.
While female is not empty, repeat:
1. Remove a person f from the front of females.
2. Write f to output.
While males is not empty, repeat:
1. Remove a person m from the front of males.
2. Write mm to output.
Terminate.

  
package queues;

import java.io.BufferedReader;
import java.io.BufferedWriter;
import java.io.FileReader;
import java.io.FileWriter;
import java.io.IOException;
import java.util.LinkedList;
import java.util.Scanner;

public class Demerge {

    public static Person readPerson(BufferedReader input) throws IOException {
        if (input.ready()) {
            String s = input.readLine();

            System.out.println("String is " + s);
            Scanner lineScanner = new Scanner(s);
            String fem = lineScanner.next();
            boolean female = false;
            if (fem.equals("F")) female = true;
            int age = lineScanner.nextInt();
            String fN = lineScanner.next();
            String lN = lineScanner.next();
            lineScanner.close();
            return new Person(female, age, fN, lN);
        }
        return null;
    }

    public static void writePerson(BufferedWriter output, Person p) throws IOException {
        output.write(p.toString() + "\n");
        output.flush();
    }

    public static void reSort(BufferedReader input, BufferedWriter output) throws IOException {
        // Copy a file of person records from input to output,
        // rearranged such that females precede males but their
        // order is otherwise unchanged.
        java.util.Queue<Person> // have to include this to avoid confusion with
                // our own Queue interface which is in this folder
                females = new LinkedList<Person>();
        java.util.Queue<Person> males = new LinkedList<Person>();
        for (; ; ) {
            Person p = readPerson(input);
            // System.out.println("read person " + p);
            if (p == null) break; // end of input
            if (p.isFemale()) females.add(p); // java.util.Queue method is add, not addLast
            else males.add(p);
        }
        while (!females.isEmpty()) {
            Person f = females.remove(); // java.util.Queue again
            writePerson(output, f);
        }
        while (!males.isEmpty()) {
            Person m = males.remove();
            writePerson(output, m);
        }
    }

    public static void main(String[] args) throws IOException {
        BufferedReader input = new BufferedReader(new FileReader("people.txt"));
        BufferedWriter output = new BufferedWriter(new FileWriter("results.txt"));

        reSort(input, output);
        input.close();
        output.close();
    }
}

A queue ADT: requirements, contract

Requirements

it must be possible to make a queue empty
it must be possible to test whether a queue is empty
it must be possible to obtain the size of a queue
it must be possible to add an element at the rear of a queue
it must be possible to remove the front element from a queue
it must be possible to access the front element in a queue without removing it

Contract

Possible contract for homogeneous queues, expressed as a Java generic interface:

  
package queues;

public interface Queue<E> {
    // Each Queue<E> object is a homogeneous queue
    // whose elements are of type E.
    /////////////// Accessors ///////////////
    public boolean isEmpty();

    // Return true if and only if this queue is empty.
    public int size();

    // Return this queues size.
    public E getFirst();

    // Return the element at the front of this queue.
    ////////////// Transformers //////////////
    public void clear();

    // Make this queue empty.
    public void addLast(E it);

    // Add it as the rear element of this queue.
    public E removeFirst();
    // Remove and return the front element of this queue.
}

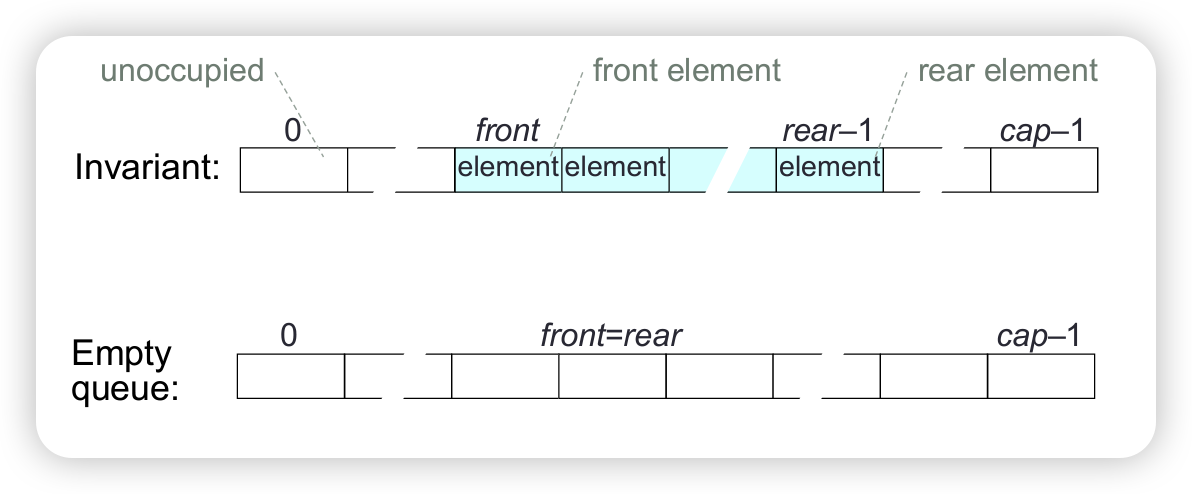
Implementations Of Queues Using Arrays

Consider representing a bounded queue, size <= cap, by:

variable size, front, rear
an array elems of length cap, containing the elements in elems[front...rear-1]

Once the rightmost array slot is occupied, no more elements can be added, unless we shift elements to fill up any unoccupied leftmost slots. But then operation addLast would have time complexity O(n), rather than O(1).

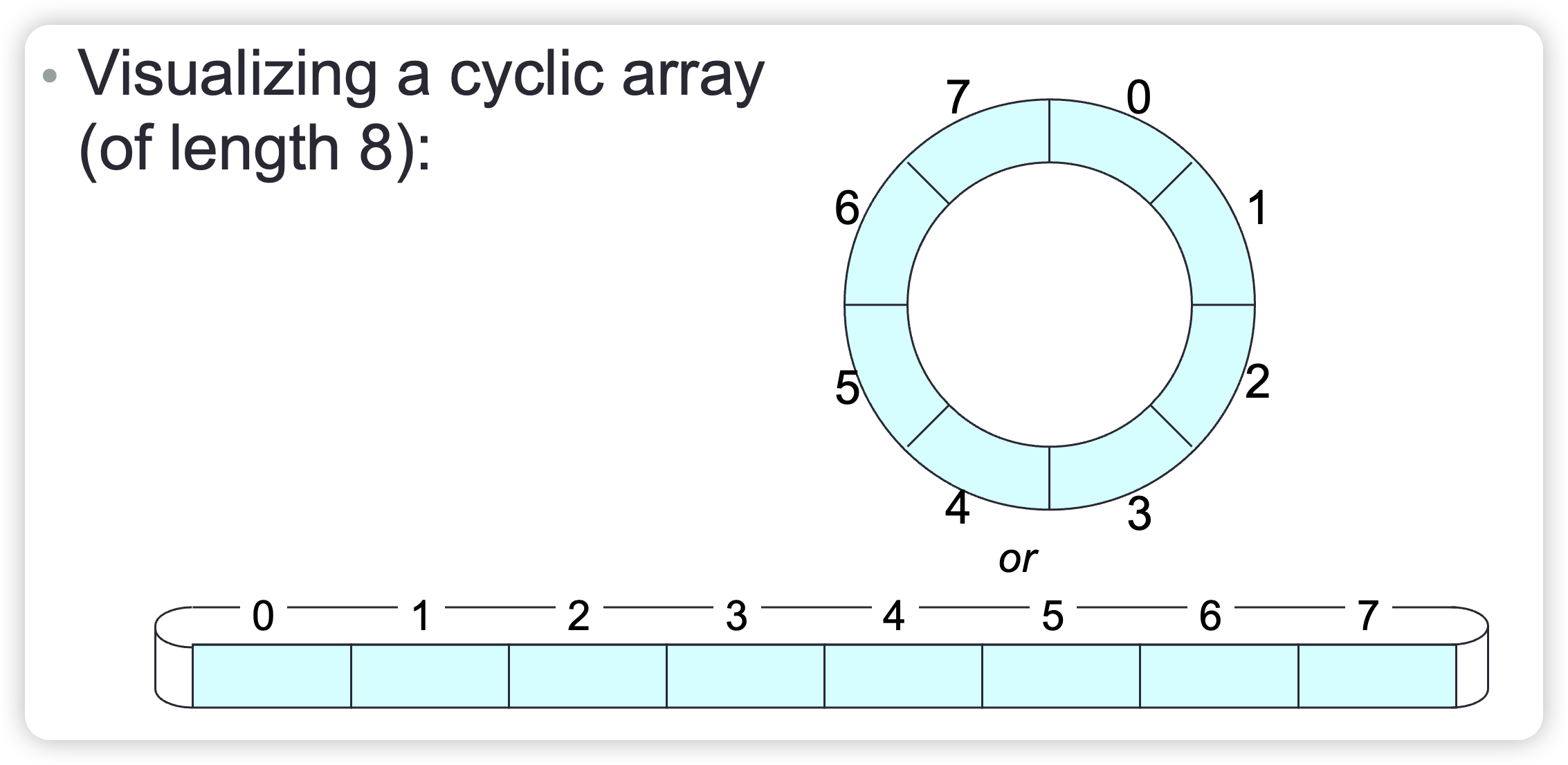
We can avoid this if we use a “cyclic array” instead of an ordinary array.

In a cyclic array a of length n, every slot has both a successor and a predecessor, in particular:

the successor of a[n-1] is a[0]
the predecessor of a[0] is a[n-1]

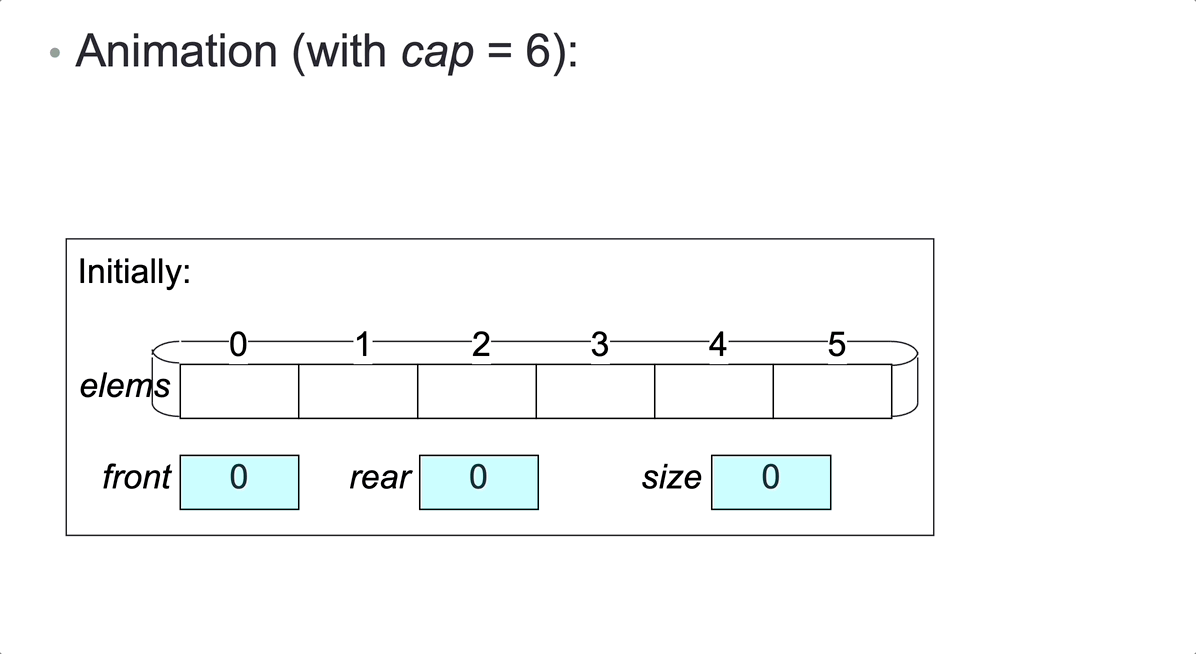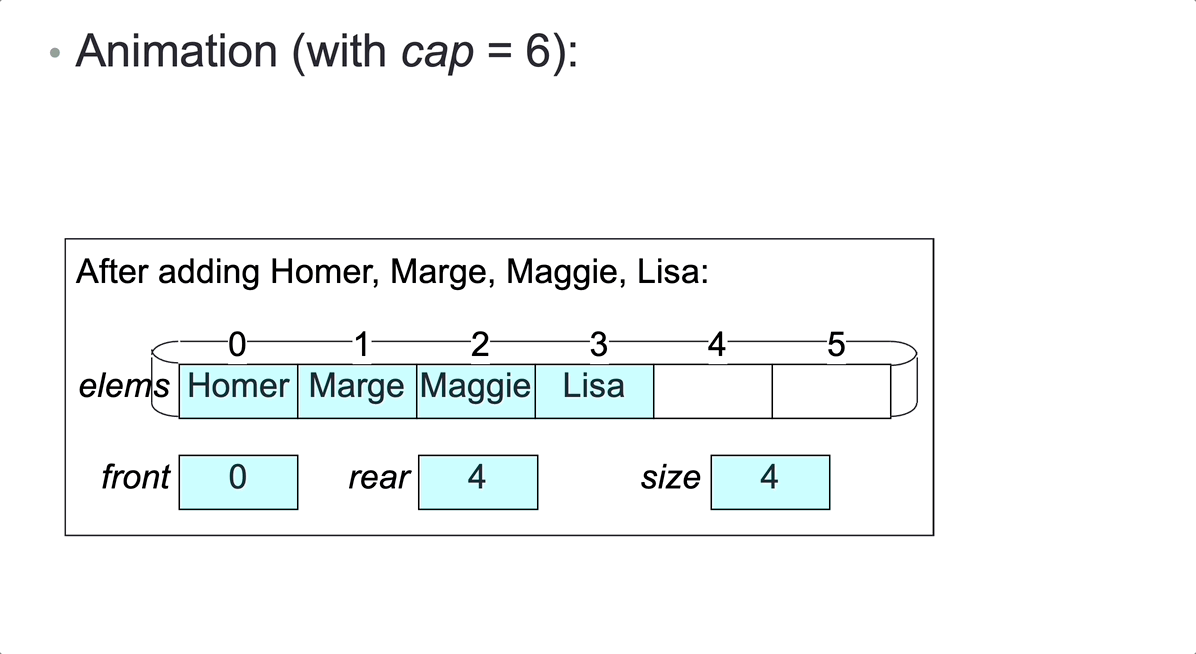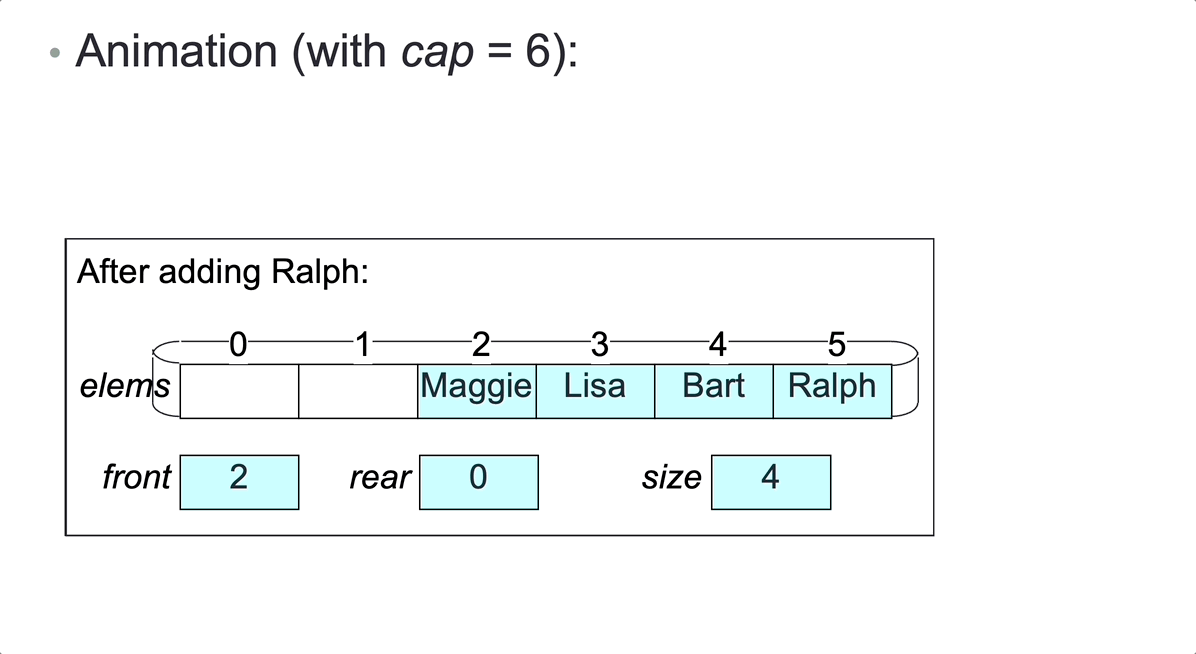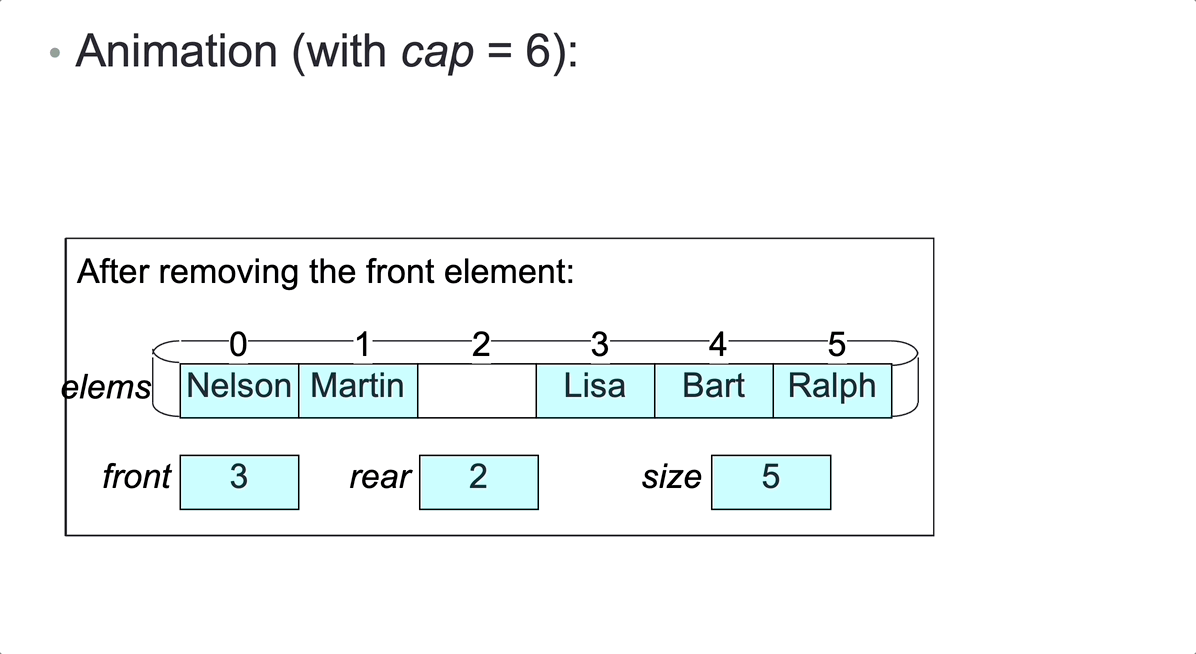
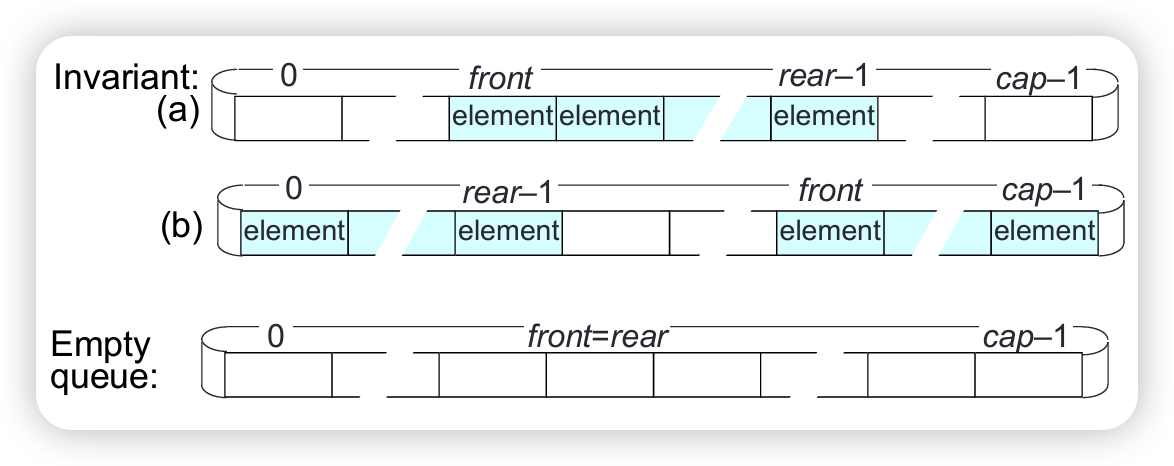
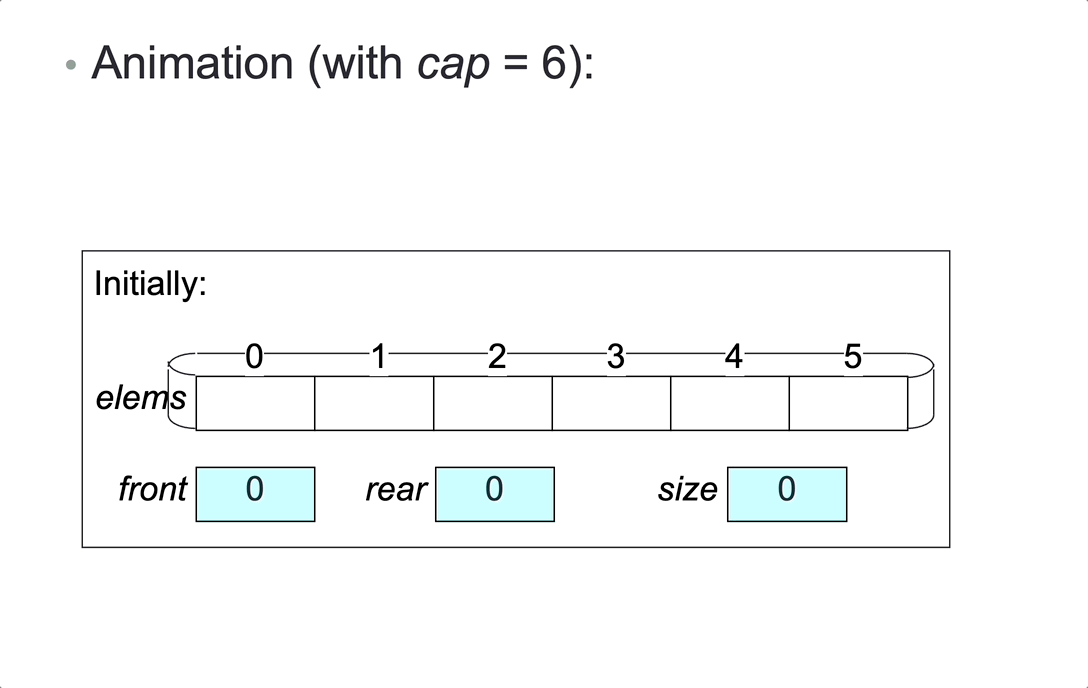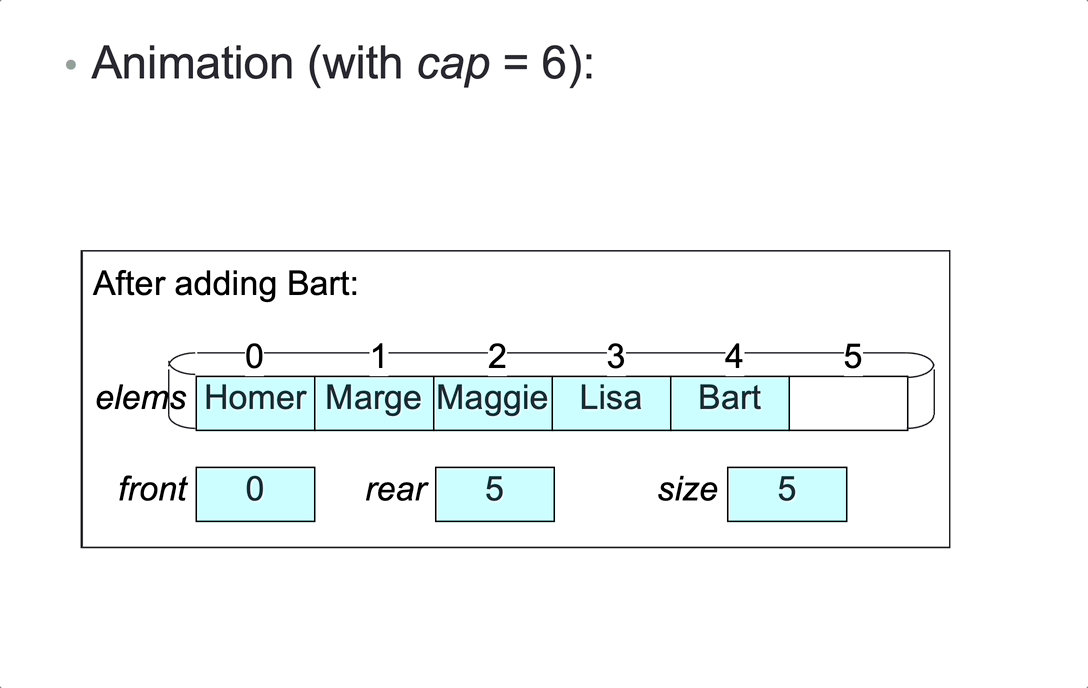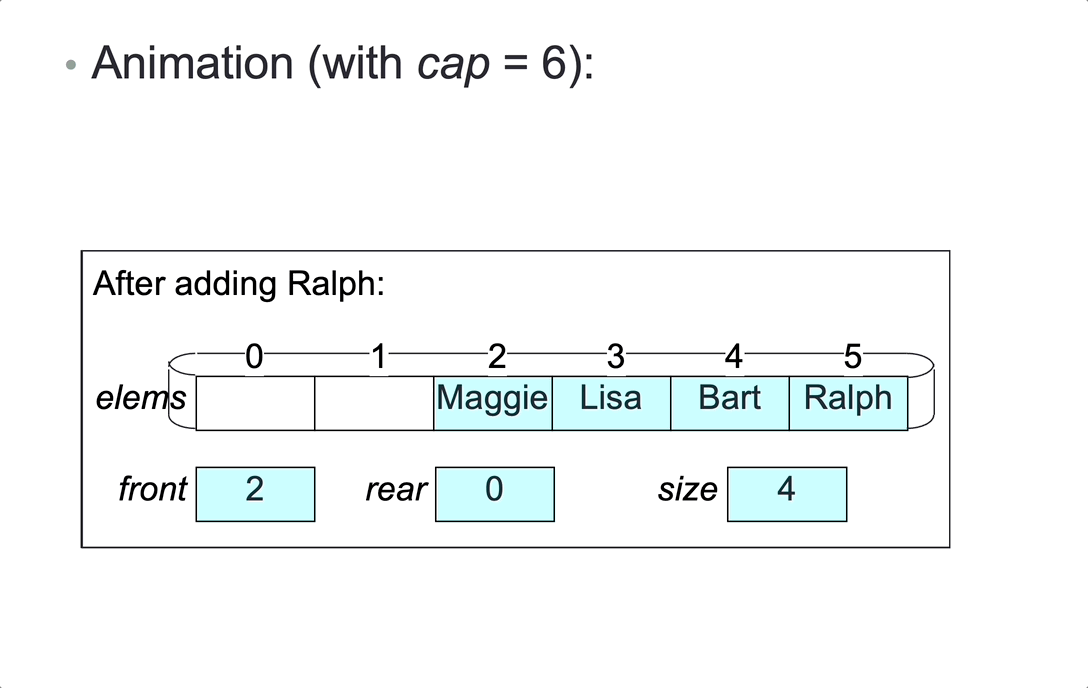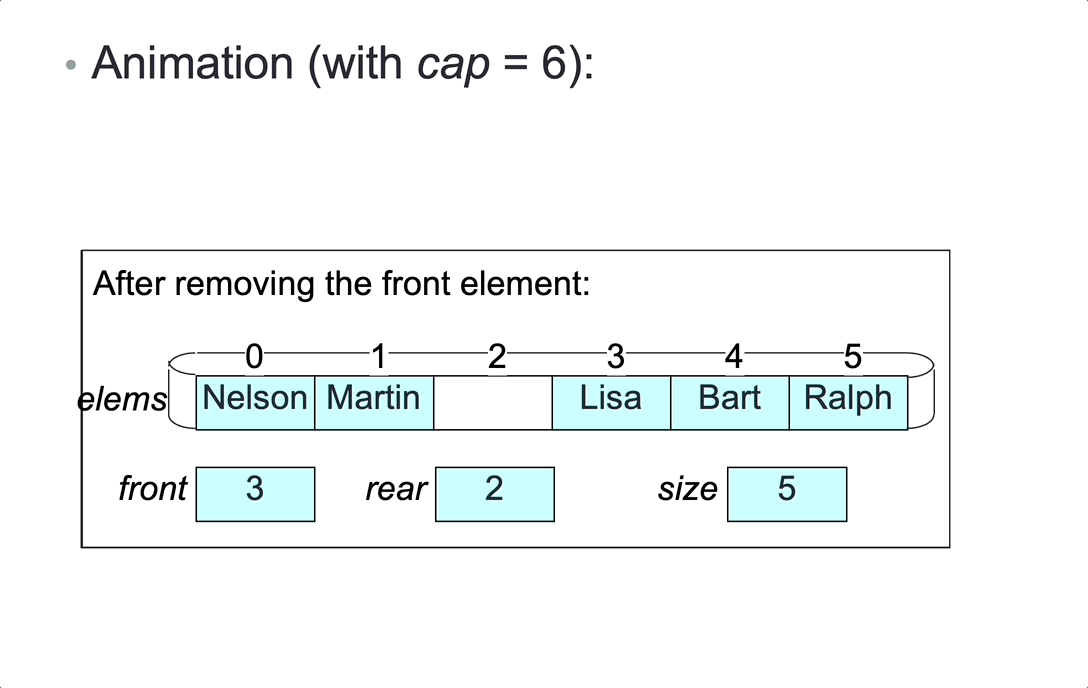
Represent a bounded queue, size <= cap, by:

variable size, front, rear
a cyclic array elems of length cap, containing the elements in either a in elems[front...rear-1] or b in elems[front...cap-1] and elems[0...rear-1].

  
package queues;

import java.util.NoSuchElementException;

public class ArrayQueue<E> implements Queue<E> {
    private E[] elems;
    private int size, front, rear;

    // ///////////// Constructor ///////////////
    @SuppressWarnings("unchecked")
    public ArrayQueue(int cap) {
        elems = (E[]) new Object[cap];
        size = front = rear = 0;
    }

    // ///////////// Accessors ///////////////
    public boolean isEmpty() {
        return (size == 0);
    }

    public int size() {
        return size;
    }

    public E getFirst() {
        if (size == 0) throw new NoSuchElementException();
        return elems[front];
    }

    // ////////////Transformers ///////////////
    @Override
    public void clear() {
        size = front = rear = 0;
    }

    public void addLast(E it) {
        if (size == elems.length) throw new ArrayIndexOutOfBoundsException();
        elems[rear++] = it;
        if (rear == elems.length) rear = 0;
        size++;
    }

    public E removeFirst() {
        if (size == 0) throw new NoSuchElementException();
        E frontElem = elems[front];
        elems[front++] = null;
        if (front == elems.length) front = 0;
        size--;
        return frontElem;
    }
}

Implementations Of Queues Using SLL

Represent an unbounded queue by:

an SLL, whose header contains links to the first node (front) and last node (rear).
a variable size (optional).

  
package queues;

import java.util.NoSuchElementException;

public class LinkedQueue<E> implements Queue<E> {
    private Node<E> front, rear;
    private int size;

    /////////////// Inner class ///////////////
    private static class Node<E> {
        public E element;
        public Node<E> next;

        public Node(E x, Node<E> s) {
            element = x;
            next = s;
        }
    }

    /////////////// Constructor ///////////////
    public LinkedQueue() {
        front = rear = null;
        size = 0;
    }

    /////////////// Accessors ///////////////
    @Override
    public boolean isEmpty() {
        return (front == null);
    }

    @Override
    public int size() {
        return size;
    }

    @Override
    public E getFirst() {
        if (front == null) throw new NoSuchElementException();
        return front.element;
    }

    ////////////// Transformers ///////////////
    @Override
    public void clear() {
        front = rear = null;
        size = 0;
    }

    @Override
    public void addLast(E it) {
        Node<E> newest = new Node<E>(it, null);
        if (rear != null) rear.next = newest;
        else front = newest;
        rear = newest;
        size++;
    }

    @Override
    public E removeFirst() {
        if (front == null) throw new NoSuchElementException();
        E frontElem = front.element;
        front = front.next;
        if (front == null) rear = null;
        size--;
        return frontElem;
    }
}

Deque

A doubly ended queue (Deque) allows elements to be added or removed at both ends of the queue. In other words, it supports the following operations in addition to the usual queue operations:

d.addFirst(x) adds x at the front the Deque d
d.getLast() retrieves the element at the rear of Deque d

Write a Deque contract in the form of a Java interface named Deque. Write a linked implementation of a Deque as a Java class LinkedDeque. Make sure that all Deque operations have time complexity O(1).

  
package queues;

public interface Deque<E> extends Queue<E> {

    public void addFirst(E it);

    // add it to front of deque

    public E removeLast();

    // Remove and return the rear element of this queue.

    public E getLast();
    // Return the element at the rear of this queue.

}

Summary of Terms

Week 8: Lists

List concepts
List applications
A list ADT: requirements, contract
Iterators
Implementations of lists: using arrays and linked-lists
Lists in the Java class library

List Concepts

A list is a sequence of elements, in a fixed order. Elements can be added/removed at any position. Elements are in position 0(leftmost), 1, 2 … n. The size of a list is the number of elements. The concatenation of lists l1 and l2 is a list containing all elements of l1 followed by all elements of l2. We can traverse a list or iterate over the list, meaning visit each of the list’s elements in turn.

Do not confuse the list abstract data type with linked-list data structure. A list ADT can be implemented using different data structures, such as arrays and linked-lists. Conversely, linked-list data structures can be used to implement many different ADT, such as stacks, queues, lists, sets.

List Applications

a sentence is a list of words, the words are in the order they are read or spoken.
an itinerary is a list of places visited on a tour, the places are in the order they are visited.
a log is a list of events records, e.g., equipment faults, the events records are in time order.

Example: simple text editor

Consider a simple text editor that supports insertion and deletion of complete lines only. The user can load text from a file, or save the text to a file. The user can select any line of the text, directly by pointing at it, or giving a line number, or by searching for a line matching a given search string. The user can delete the selected line. The user can insert a new line, either above the selected line or below the selected line.

We can represent the text being edited by:

a list of lines, text
the position sel of the selected line

We can implement the user commands straightforwardly in terms of list operations:

Delete: remove the line at position sel in text.
Insert above: add the new line at position sel in text, then increment sel.
Insert below: increment sel, then add the new line at position sel in text.
Save: traverse text, writing each line to the output file.

- A list ADT: requirements, contract

Requirements

it must be possible to make a list empty
it must be possible to test whether a list is empty
it must be possible to obtain the length of a list
it must be possible to add an element at any position in a list
it must be possible to remove the element at any position in a list
it must be possible to inspect or update the element at any position in a list
it must be possible to concatenate lists
it must be possible to test lists for equality
it must be possible to traverse a list

Contract

Possible contract for homogeneous lists:

  
package lists;

import java.util.Iterator;

public interface List<E> extends Iterable<E> {
    // Each List<E> object is a homogeneous list
    // whose elements are of type E.
    // ////////// Accessors ////////////
    public boolean isEmpty();

    // Return true if and only if this list is empty.
    public int size();

    // Return this list�s length.
    public E get(int p);

    // Return the element at position p in this list.
    public boolean equals(List<E> that);

    // Return true if and only if this list and that have the
    // same length, and each element of this list equals
    // the corresponding element of that.
    // //////////Transformers ////////////
    public void clear();

    // Make this list empty.
    public void set(int p, E it);

    // Replace the element at position p in
    // this list by it.
    public void add(int p, E it);

    // Add it at position p in this list.
    public void addLast(E it);

    // Add it after the last element of this list.

    public void addAll(List<E> that);

    // Add all the elements of that after the
    // last element of this list.
    public E remove(int p);

    // Remove and return the element at
    // position p in this list.
    //////////// Iterator ////////////
    @Override
    public Iterator<E> iterator();
    // Return an iterator that will visit all
    // elements of this list, in left-to-right order.

}

Traversal

To traverse array:

  
for (int i = 0; i < array.length; i++) {
    // process array[i]
    ...array[i]...
}

This traversal has time complexity O(n). We could mimic this to traverse list:

  
for (int i = 0; i < list.size(); i++) {
    // process list.get(i)
    ...list.get(i)...
    ...list.set(p, it)...
}

However this traversal could have time complexity O(n^2), if get and set turn out to be O(n).

To improve this, we can use an Iterator to traverse list:

  
// constructs an iterator over the element of list
Iterator<T> it = list.iterator();

while (it.hasNext()) { // tests whether that iterator still has more elements to visit
    T elem = it.next(); // visits the next element in that iterator
    ...elem...
}

View an Iterator as a path along which we visit the elements one by one, in some desired order.

Iterator Implementation

An Iterator is represented by a position on The Iterator’s path, typically:

an index if the elements are held in an array
a link if the elements are held in a linked-list

The hasNext() operation tests whether there is a next position on the Iterator’s path. The next() operation advances to the next position on the Iterator’s path, and returns the elements at that position, it throws an exception if there is no next position.

Using Arrays

Represent a bounded list, size <= cap, by:

a variable size
an array elems of length cap, containing the elements in elems[0...size-1]

  
package lists;

import java.util.Iterator;
import java.util.NoSuchElementException;

public class ArrayList<E> implements List<E> {
    private E[] elems;
    private int size;

    // ////////// Constructor ////////////
    @SuppressWarnings("unchecked")
    public ArrayList(int cap) {
        elems = (E[]) new Object[cap];
        size = 0;
    }

    public ArrayList() {
        this(10);
    }

    @Override
    public boolean isEmpty() {

        return (size == 0);
    }

    @Override
    public int size() {
        return size;
    }

    // Return the element at position p in this list.
    @Override
    public E get(int p) {
        if (p < 0 || p >= size) throw new NoSuchElementException();
        return elems[p];
    }

    // Return true if and only if this list and that have the
    // same length, and each element of this list equals
    // the corresponding element of that.
    @Override
    public boolean equals(List<E> that) {
        if (that.size() != size) return false;
        for (int i = 0; i < size; i++) {
            if (!this.get(i).equals(that.get(i))) return false;
        }
        return true;
    }

    // Make this list empty.
    @Override
    public void clear() {
        size = 0;
    }

    // Replace the element at position p in
    // this list by it.
    @Override
    public void set(int p, E it) {
        if (p < 0 || p >= size) throw new NoSuchElementException();
        else elems[p] = it;
    }

    // Add it at position p in this list
    // if no room, double size of the array
    @Override
    public void add(int p, E it) {
        if (size == elems.length) this.doubleArray();
        for (int i = size; i >= p; i--) elems[i + 1] = elems[i];
        elems[p] = it;
        size++;
    }

    // Add it after the last element of this list.
    @Override
    public void addLast(E it) {
        elems[size++] = it;
    }

    // Add all the elements of that after the
    // last element of this list.
    @Override
    public void addAll(List<E> that) {
        int newCapacity = this.size() + that.size();
        while (elems.length < newCapacity) doubleArray();
        for (int j = 0; j < that.size(); j++) elems[size + j] = that.get(j);
    }

    public E[] getElems() {
        return elems;
    }

    public void setElems(E[] elems) {
        this.elems = elems;
    }

    public int getSize() {
        return size;
    }

    public void setSize(int size) {
        this.size = size;
    }

    // Remove and return the element at
    // position p in this list.
    @Override
    public E remove(int p) {
        E val = elems[p];
        for (int i = p + 1; i < size; i++) elems[i] = elems[i + 1];
        size--;
        return val;
    }

    // return an iterator that will visit all
    // elements of this list, in left-to-right order.
    @Override
    public Iterator<E> iterator() {
        return new LRIterator();
    }

    // //////////Inner class ////////////
    public class LRIterator implements Iterator<E> {
        private int position;

        // position is the index of the slot containing the
        // next element to be visited.
        private LRIterator() {
            position = 0;
        }

        @Override
        public boolean hasNext() {
            return (position < size);
        }

        @Override
        public E next() {
            if (position >= size) throw new NoSuchElementException();
            return elems[position++];
        }

        @Override
        public void remove() {
            // omitting this one

        }
    }

    public void doubleArray() {
        int doub = 2 * elems.length;
        @SuppressWarnings("unchecked")
        E[] newElems = (E[]) new Object[doub];
        for (int i = 0; i < size; i++) newElems[i] = elems[i];
        elems = newElems;
    }
}

Since LRIterator is a non-static inner class of ArrayList, its methods can access ArrayList instance variables:

Using SLL

Represent an unbounded list by:

a variable size
an SLL, with links to both the first and last nodes

  
package lists;

import java.util.Iterator;
import java.util.NoSuchElementException;

public class LinkedList<E> implements List<E> {
    // Each List<E> object is a homogeneous list
    // whose elements are of type E.
    // ////////// Accessors ////////////

    private Node<E> first, last;
    private int size;

    // ////////// Inner class ////////////
    private static class Node<E> {
        public E element;
        public Node<E> next;

        public Node(E x, Node<E> s) {
            element = x;
            next = s;
        }
    }

    // ////////// Constructor ////////////
    public LinkedList() {
        first = last = null;
        size = 0;
    }

    // Return true if and only if this list is empty.
    @Override
    public boolean isEmpty() {
        return size == 0;
    }

    // Return this list's length.
    @Override
    public int size() {
        return size;
    }

    // ///////// Auxiliary method ///////////
    private Node<E> locate(int p) {
        // Return a link to the node at position p in this list.
        Node<E> curr = first;
        for (int j = 0; j < p; j++) curr = curr.next;
        return curr;
    }

    // Return the element at position p in this list.
    @Override
    public E get(int p) {
        if (p < 0 || p >= size) throw new NoSuchElementException();
        return locate(p).element;
    }

    // Return true if and only if this list and that have the
    // same length, and each element of this list equals
    // the corresponding element of that.
    @Override
    public boolean equals(List<E> that) {
        if (this.size != that.size()) return false;
        boolean same = true;

        Node<E> position1 = this.first; // position in the first list
        int index = 0; // position in the second list
        while (position1 != null && same) {
            if (position1.element != that.get(index)) same = false;
            else {
                position1 = position1.next;
                index++;
            }
        }
        return same;
    }

    public Node<E> getFirst() {
        return first;
    }

    public void setFirst(Node<E> first) {
        this.first = first;
    }

    public Node<E> getLast() {
        return last;
    }

    public void setLast(Node<E> last) {
        this.last = last;
    }

    // //////////Transformers ////////////

    // Make this list empty.
    @Override
    public void clear() {
        first = last = null;
        size = 0;
    }

    // Replace the element at position p in
    // this list by it.
    @Override
    public void set(int p, E it) {
        if (size == 0 || size <= p) throw new NoSuchElementException();
        Node<E> temp = new Node<E>(it, null);
        if (p == 0) {
            temp.next = first.next;
            first = temp;
            if (size == 1) last = temp;
        } else {
            Node<E> temp1 = first;
            for (int i = 0; i < p - 1; i++)
                temp1 = temp1.next; // identified node before replacement point
            Node<E> temp2 = temp1.next.next; // node after replacement point
            temp1.next = temp;
            temp.next = temp2;
            if (p == size - 1) last = temp; // if replacing final node
        }
    }

    // Add it at position p in this list.
    @Override
    public void add(int p, E it) {
        Node<E> temp = new Node<E>(it, null);
        if (size == 0) {
            first = last = temp;
            size++;
        } else {
            if (p == size) addLast(it);
            else {
                Node<E> temp1 = locate(p - 1);
                Node<E> temp2 = temp1.next;
                temp1.next = temp;
                temp.next = temp2;
                size++;
            }
        }
    }

    // Add it after the last element of this list.
    @Override
    public void addLast(E it) {
        Node<E> temp = new Node<E>(it, null);
        if (size == 0) {
            first = last = temp;
            size++;
        } else {
            last.next = temp;
            last = temp;
            size++;
        }
    }

    // Add all the elements of that after the
    // last element of this list.
    @Override
    public void addAll(List<E> that) {
        if (!that.isEmpty()) {
            for (E e : that) addLast(e);
        }
    }

    // Remove and return the element at
    // position p in this list.
    @Override
    public E remove(int p) {
        if (size == 0 || size <= p) throw new NoSuchElementException();
        else {
            if (size == 1) {
                E e = first.element;
                first = last = null;
                size--;
                return e;
            }
            // are we removing the head?
            if (p == 0) {
                E e = first.element;
                first = first.next;
                size--;
                return e;
            }
            Node<E> precursor = locate(p - 1);
            E e = precursor.next.element;
            precursor.next = precursor.next.next;
            // did we remove the tail?
            if (p == size - 1) last = precursor;
            size--;
            return e;
        }
    }

    // ////////// Iterator ////////////

    // Return an iterator that will visit all
    // elements of this list, in left-to-right order.
    @Override
    public Iterator<E> iterator() {
        return new LRIterator();
    }

    //////////// Inner class ////////////
    private class LRIterator implements Iterator<E> {
        // An LRIterator object is a left-to-right iterator over
        // a LinkedList<E> object.
        private Node<E> position;

        // position is a link to the node containing the next
        // element to be visited.
        private LRIterator() {
            position = first;
        }

        @Override
        public boolean hasNext() {
            return (position != null);
        }

        @Override
        public E next() {
            if (position == null) throw new NoSuchElementException();
            E nextElem = position.element;
            position = position.next;
            return nextElem;
        }

        @Override
        public void remove() {
            // not implemented
        }
    }
}

Since LRIterator is a non-static inner class of LinkedList, its methods can access LinkedList instance variables:

Summary of List Implementations

Operation	Array representation	SLL representation
`get`	O(1)	O(p)
`set`	O(1)	O(p)
`remove`	O(n)	O(p)
`add`	O(n)	O(p)
`addLast` (best)	O(1)	O(1)
`addLast` (worst)	O(n)	O(1)
`equals`	O(n)	O(n)
`addAll`	O(n’)	O(1)

Time complexities of the principal list methods for lists in the Java class library:

Method	ArrayList	LinkedList
`get`	O(1)	O(p)
`set`	O(1)	O(p)
`remove`	O(n)	O(p)
`add`	O(n)	O(p)
`addLast` (best)	O(1)	O(1)
`addLast` (worst)	O(n)	O(1)
`addLast` (amortized)	O(1)	O(1)

Amortized Complexity

An operation’s amortized time complexity reflects its performance averaged over a large number of calls. Consider the addLast method in ArrayList, normally only 1 copy is needed. When the array is full, n elements are copied into a new array with doubled length, so in total n+1 copies are needed.

Consider 30 consecutive additions to an empty list with initial capacity 4.

Number of copies:

1, 1, 1, 1, 5, 1, 1, 1, 9, 1, 1, 1, 1, 1, 1, 1, 17, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1

Total 58

On average, 2 copies per call. Amortized time complexity is O(1).

Example: simple text editor

  
package lists;

import java.io.BufferedReader;
import java.io.BufferedWriter;
import java.io.FileReader;
import java.io.FileWriter;
import java.io.IOException;
import java.util.NoSuchElementException;

public class TextEditor {
    private List<String> text;
    private int sel; // position of the selected line

    public TextEditor() {
        // Make the text empty.
        // text = new ArrayList<String>(); //delete as appropriate
        text = new LinkedList<String>();
        sel = -1;
    }

    public void select(int p) {
        // Select the line at position p.
        if (p < 0 || p >= text.size()) throw new NoSuchElementException();
        sel = p;
    }

    public void delete() {
        // Delete the selected line.
        if (sel < 0) throw new NoSuchElementException();
        text.remove(sel);
        if (sel == text.size()) sel--;
    }

    public void find(String str) {
        // Select the next line containing str as a substring.
        // Wrap round to line 0 if necessary.
        if (sel < 0) throw new NoSuchElementException();
        int p = sel, n = text.size();
        do {
            String line = text.get(p);
            if (line.indexOf(str) >= 0) {
                // � str found
                sel = p;
                // System.out.println("Found string at line " + p);
                return;
            }
            if (++p == n) p = 0;
        } while (p != sel);
        throw new NoSuchElementException(); // str not found
    }

    public void insertAbove(String line) {
        // Insert line immediately above the selected line.
        if (sel < 0) throw new NoSuchElementException();
        text.add(sel, line);
        sel++;
    }

    public void insertBelow(String line) {
        // Insert line immediately below the selected line.
        sel++;
        text.add(sel, line);
    }

    public void load(BufferedReader input) throws IOException {
        // Load the entire contents of input into the text.
        for (; ; ) {
            String line = input.readLine();
            if (line == null) break;
            text.addLast(line);
        }
        sel = text.size() - 1; // select last line
    }

    public void save(BufferedWriter output) throws IOException {
        // Save the text to output.
        for (String line : text) output.write(line + "\n");
    }

    public static void main(String[] args) throws IOException {
        TextEditor theText = new TextEditor();
        BufferedReader input = new BufferedReader(new FileReader("jungleBook.txt"));
        BufferedWriter output = new BufferedWriter(new FileWriter("jungleResults.txt"));

        theText.load(input);
        theText.find("Mother"); // select the line containing mother
        theText.insertAbove("This is inserted text: ignore it!");
        theText.save(output);

        input.close();
        output.close();
    }
}

Week 9: Sets

Set concepts
Set applications
A set ADT: requirements, contract
Implementations of sets: using member arrays, boolean arrays and linked-lists
Sets in the Java class library

Set concepts

A set is a collection of elements, with no duplicates, and in no fixed order. An element does not have a “position” in the set.

The elements of a set are usually called its members.

Mathematical notation for sets:

{a, b, …, z} is the set whose members are a, b, …, z. (The members can be written in any order.)
{} is the empty set.

Note: We can use this notation in algorithms, but it is not supported by Java.

The size or cardinality of a set s is the number of members of s. This is written #s. For example, #NAFTA = 3, #{red, white, red} = #{red, white} = 2, duplicates are not counted.

An empty set has no members. We can test whether x is a member of set s. This is the membership test, written x ∈ s.

Two sets are equal if they contain exactly the same members. NAFTA = {US, CA, MX}, order of members is not significant. NAFTA != {CA, US}, these sets are not equal.

Set s1 subsumes set s2 or s1 is a superset of s2, or s2 is a subset of s1 if every member of s2 is also a member of s1. This is written s2 ⊆ s1.

The union of sets s1 and s2 is a set containing just those values that are members of s1 or s2 or both. This is written s1 ∪ s2.

The intersection of sets s1 and s2 is a set containing just those values that are members of both s1 and s2. This is written s1 ∩ s2.

Two sets are disjoint if they have no common member, if their intersection is empty.

The difference of sets s1 and s2 is a set containing just those values that are members of s1 but not of s2. This is written s1 - s2.

Set Applications

Spell-checker: a spell-checker’s dictionary is a set of words. A spell-checker highlights any words in a document that are not members of its dictionary. Some spell-checkers allow users to add words to their dictionaries.

Relational database: a relational database table is essentially a set of tuples. Each tuple is distinct. The tuples have no particular order.

Example: prime numbers

A prime number is an integer that is divisible only by itself and 1.

Eratosthenes’s sieve algorithm:

To compute the set of prime numbers less than n where n > 0:

Set sieve = {2, 3, ...,n-1}
For i = 2, 3,..., while i^2 < n, repeat:
1. If i is a member of sieve, remove all multiplies of i from sieve.
Terminate yielding sieve.

Set ADT: requirements, contract

Requirements

it must be possible to make a set empty
it must be possible to test whether a set is empty
it must be possible to obtain the size of a set
it must be possible to perform a membership test
it must be possible to add or remove a member
it must be possible to test whether two sets are equal
it must be possible to test whether one set subsumes another
it must be possible to compute the union, intersection, or difference of two sets
it must be possible to traverse a set

Contract

  
package sets;

import java.util.Iterator;

public interface Set<E> extends Iterable<E> {
    // Each Set<E> object is a homogeneous set whose
    // members are of type E.
    //////////// Accessors ////////////
    public boolean isEmpty(); // Return true if and only if this set is empty.

    public int size(); // Return the size of this set.

    public boolean contains(E it);

    // Return true if and only if it is a member of this set.

    public boolean equals(Set<E> that);

    // Return true if and only if this set is equal to that.

    public boolean containsAll(Set<E> that);

    // Return true if and only if this set subsumes that.

    //////////// Transformers ////////////

    public void clear(); // Make this set empty.

    public void add(E it); // Add it as a member of this set.

    // Do nothing if it is already a member of this set.

    public void remove(E it); // Remove it from this set.

    // Do nothing if it is not a member of this set.

    public void addAll(Set<E> that); // Make this set the union of itself and that.

    //////////// Transformers ////////////

    public void removeAll(Set<E> that); // Make this set the difference of itself and that.

    public void retainAll(Set<E> that); // Make this set the intersection of itself and that.

    //////////// Iterator ////////////

    @Override
    public Iterator<E> iterator(); // Return an iterator that will visit all members of this
    // set, in no particular order

}

Implementations of Sets Using Member Arrays

Represent a bounded set, size <= cap, by:

a variable size, containing the current size
a sorted array members of length cap, containing the set members in members[0...size-1] with no duplicates

  
package sets;

import java.util.Iterator;
import java.util.NoSuchElementException;

public class ArraySet<E extends Comparable<E>> implements Set<E> {
    private E[] elems;
    private int size;

    @SuppressWarnings("unchecked")
    public ArraySet(int cap) {
        elems = (E[]) new Comparable[cap];
        size = 0;
    }

    @Override
    public boolean isEmpty() {
        return (size == 0);
    }

    @Override
    public int size() {
        return size;
    }

    // uses binary search
    @Override
    public boolean contains(E it) {
        int position = binarySearch(it);
        return (position != -1);
    }

    // Return true if and only if this set is equal to that.
    // uses pairwise comparison
    @Override
    public boolean equals(Set<E> that) {
        if (this.size() != that.size()) return false;
        Iterator<E> members = that.iterator(); // iterator on second set
        for (E it : this) {
            if (members.hasNext()) {
                E member = members.next();
                if (!it.equals(member)) return false;
            }
        }
        return true;
    }

    // Return true if and only if this set subsumes that.
    // uses variant of pairwise comparison
    @Override
    public boolean containsAll(Set<E> that) {
        Iterator<E> members = this.iterator(); // iterator on first set
        for (E it : that) {

            boolean found = false;
            while (!found) {
                if (!members.hasNext()) return false;
                else {
                    E temp = members.next();
                    if (temp.equals(it)) found = true;
                    if (it.compareTo(temp) < 0) return false;
                }
            }
        }
        return true;
    }

    @Override
    public void clear() {
        size = 0;
    }

    // Add it as a member of this set.
    // Do nothing if it is already a member of this set.
    // uses (variant of) binary search, plus insertion
    @Override
    public void add(E it) {
        if (size == elems.length) throw new ArrayIndexOutOfBoundsException();
        int position = -1; // where to place this item, if appropriate
        if (size == 0) position = 0;
        // find the index of the first element greater than it
        else {
            int l = 0, r = size - 1;

            // do binary search to find position to place
            while (l <= r) {
                int m = (l + r) / 2;
                int comp = it.compareTo(elems[m]);
                if (comp == 0) return; // element is already there, don't add
                else if (comp < 0) {
                    if (m == 0) {
                        position = 0;
                        l = r + 1; // get out of the loop, will add to start of array
                    } else {
                        int comp2 = it.compareTo(elems[m - 1]);
                        if (comp2 > 0) {
                            position = m;
                            l = r + 1; // get out of the loop, will add at position m
                        } else r = m - 1;
                    }

                } else { // must have comp>0
                    if (m == size - 1) {
                        position = size;
                        l = r + 1; // get out of the loop, will add to end of array
                    } else {
                        int comp2 = it.compareTo(elems[m + 1]);
                        if (comp2 < 0) {
                            position = m + 1;
                            l = r + 1; // get out of the loop, will add at position m+1
                        } else l = m + 1;
                    }
                }
            }
        }
        // add it to elems[position]
        for (int i = size; i > position; i--) elems[i] = elems[i - 1];
        elems[position] = it;
        size++;
    }

    // Remove it from this set.
    // Do nothing if it is not a member of this set.
    // uses binary search + deletion
    @Override
    public void remove(E it) {
        if (size == 0) return; // do nothing if set is empty
        int position = binarySearch(it);
        if (position == -1) return; // do nothing if it is not a member of this set
        // remove element at position p
        for (int i = position; i < size - 1; i++) elems[i] = elems[i + 1];
        elems[size - 1] = null;
        size--;
    }

    /** auxilliary method */
    public int binarySearch(E it) {
        // return position of element it
        // or -1 otherwise
        int position = -1;
        int l = 0, r = size - 1;
        while (l <= r) {
            int m = (l + r) / 2;
            int comp = it.compareTo(elems[m]);
            if (comp == 0) return m;
            else if (comp < 0) r = m - 1;
            else l = m + 1;
        }
        return position;
    }

    // Make this set the union of itself and that.
    // uses array merge (using iterator on second set)
    @Override
    public void addAll(Set<E> that) {

        Iterator<E> members = that.iterator(); // iterator on second set
        @SuppressWarnings("unchecked")
        E[] tempArray = (E[]) new Comparable[elems.length + that.size()];
        int tempCounter = 0;
        int i = 0; // position in 1st array
        E item = null; // the next item in the second set
        while (i < size) {
            if (!members.hasNext()) { // add remaining elements from this set to array
                while (i < size) {
                    tempArray[tempCounter] = elems[i];
                    i++;
                    tempCounter++;
                }
            } else {
                item = members.next();
                while (i < size && elems[i].compareTo(item) < 0) {
                    tempArray[tempCounter] = elems[i];
                    tempCounter++;
                    i++;
                }
                tempArray[tempCounter] = item;
                tempCounter++;
                if ((i < size) && elems[i].equals(item)) i++;
            }
        }
        // add any remaining elements of second set
        while (members.hasNext()) {
            tempArray[tempCounter] = members.next();
            tempCounter++;
        }
        elems = tempArray;
        size = tempCounter;
    }

    // Make this set the difference of itself and that.
    // variant of array merge
    // use iterator on second set
    @Override
    public void removeAll(Set<E> that) {
        Iterator<E> members = that.iterator(); // iterator on second set
        @SuppressWarnings("unchecked")
        E[] tempArray = (E[]) new Comparable[elems.length];
        int tempCounter = 0;
        int i = 0; // position in 1st array
        E item = null; // the next item in the second set
        while (i < size) {
            if (!members.hasNext()) { // add remaining elements from this set to array
                // nothing more to remove
                while (i < size) {
                    tempArray[tempCounter] = elems[i];
                    i++;
                    tempCounter++;
                }
            } else {
                item = members.next();
                while (elems[i].compareTo(item) < 0) {
                    // these elements are not in the second set, so keep
                    tempArray[tempCounter] = elems[i];
                    tempCounter++;
                    i++;
                }

                if (elems[i].equals(item)) i++; // skip this element, as in second set
            }
        }
        elems = tempArray;
        size = tempCounter;
    }

    // Make this set the intersection of itself and that.
    // variant of array merge
    // use iterator on second set
    @Override
    public void retainAll(Set<E> that) {
        Iterator<E> members = that.iterator(); // iterator on second set
        @SuppressWarnings("unchecked")
        E[] tempArray = (E[]) new Comparable[elems.length];
        int tempCounter = 0;
        int i = 0; // position in 1st array
        E item = null; // the next item in the second set
        while (i < size && members.hasNext()) {
            item = members.next();
            while (elems[i].compareTo(item) < 0) i++; // skip along first set
            if (elems[i].equals(item)) {
                // add to the intersection
                tempArray[tempCounter] = item;
                tempCounter++;
            }
        }
        elems = tempArray;
        size = tempCounter;
    }

    // return an iterator that will visit all
    // elements of this set, in some order
    @Override
    public Iterator<E> iterator() {
        return new LRIterator();
    }

    // //////////Inner class ////////////
    private class LRIterator implements Iterator<E> {
        private int position;

        // position is the index of the slot containing the
        // next element to be visited.
        private LRIterator() {
            position = 0;
        }

        @Override
        public boolean hasNext() {
            return (position < size);
        }

        @Override
        public E next() {
            if (position >= size) throw new NoSuchElementException();
            return elems[position++];
        }

        @Override
        public void remove() {
            // omitting this one

        }
    }
}

Summary of algorithms and time complexities:

Operation	Algorithm	Time complexity
`contains`	binary search	O(log n)
`add`	binary search + insertion	O(n)
`remove`	binary search + deletion	O(n)
`equals`	pairwise comparison	O(n)
`containsAll`	variant of pairwise comparison	O(n)
`addAll`	array merge	O(n+n’)
`removeAll`	variant of array merge	O(n+n’)
`retainAll`	variant of array merge	O(n+n’)

where n’ is the size of the other set

Implementations of Sets Using SLL

Represent an unbounded set by:

a variable size
a sorted SLL, containing one member per node with no duplicates.

  
package sets;

import java.util.Iterator;
import java.util.NoSuchElementException;

// use a sorted SLL
public class LinkedSet<E extends Comparable<E>> implements Set<E> {
    private Node<E> first;
    private int size;

    // ////////// Inner class ////////////
    private static class Node<E> {
        public E element;
        public Node<E> next;

        public Node(E x, Node<E> s) {
            element = x;
            next = s;
        }
    }

    // ////////// Constructor ////////////
    public LinkedSet() {
        first = null;
        size = 0;
    }

    @Override
    public boolean isEmpty() {
        return size == 0;
    }

    @Override
    public int size() {
        return size;
    }

    // SLL linear search
    @Override
    public boolean contains(E it) {
        // Return true if and only if it is a member of this set.
        for (E elem : this) {
            if (elem.equals(it)) return true;
            if (elem.compareTo(it) > 0) return false;
        }
        return false;
    }

    // pairwise comparison
    @Override
    public boolean equals(Set<E> that) {
        if (this.size() != that.size()) return false;
        Iterator<E> members1 = this.iterator();
        Iterator<E> members2 = that.iterator();

        while (members1.hasNext() && members2.hasNext()) {
            if (!members1.next().equals(members2.next())) return false;
        }
        return true;
    }

    // variant of pairwise comparison
    @Override
    public boolean containsAll(Set<E> that) {
        if (this.size() < that.size()) return false;
        Iterator<E> members1 = this.iterator();
        Iterator<E> members2 = that.iterator();

        while (members2.hasNext()) {
            if (!members1.hasNext()) return false;
            E nextItem = members2.next();
            E compItem = null;
            while (members1.hasNext() && (compItem == null || compItem.compareTo(nextItem) < 0)) {
                compItem = members1.next();
            }
            if (!compItem.equals(nextItem)) return false;
        }
        return true;
    }

    @Override
    public void clear() {
        first = null;
        size = 0;
    }

    @Override
    // Add it as a member of this set.
    // Use SLL linear search + insertion
    public void add(E it) {
        Node<E> newNode = new Node<E>(it, null);
        // empty list
        if (first == null) {
            first = newNode;

        } else {
            // head of list has element > it
            if (first.next == null && first.element.compareTo(it) > 0) {
                newNode.next = first;
                first = newNode;
            } else {

                Node<E> curr = first;
                Node<E> succ = curr.next;
                while (succ != null && succ.element.compareTo(it) < 0) {
                    curr = succ;
                    succ = succ.next;
                }
                newNode.next = succ;
                curr.next = newNode;
            }
        }
        size++;
    }

    @Override
    // Remove it from this set.
    // Do nothing if it is not a member of this set.
    public void remove(E it) {
        if (size > 0) {
            if (first.element.equals(it)) {
                first = first.next;
                size--;
            } else {
                if (first.element.compareTo(it) > 0) return; // do nothing
                Node<E> prev = first;
                Node<E> curr = prev.next;
                while (curr != null && curr.element.compareTo(it) < 0) {
                    prev = curr;
                    curr = curr.next;
                }
                if (curr != null && curr.element.equals(it)) {
                    prev.next = curr.next;
                    size--;
                }
            }
        }
    }

    @Override
    // Make this set the union of itself and that.
    // SLL merge
    public void addAll(Set<E> that) {
        Iterator<E> members1 = this.iterator();
        Iterator<E> members2 = that.iterator();
        while (members1.hasNext() && members2.hasNext()) {
            E element1 = members1.next();
            // continue here!
            //
            //

        }
    }

    @Override
    // Make this set the difference of itself and that.
    // variant of SLL merge
    public void removeAll(Set<E> that) {
        // TODO Auto-generated method stub

    }

    @Override
    // Make this set the intersection of itself and that.
    // variant of SLL merge
    public void retainAll(Set<E> that) {
        // TODO Auto-generated method stub

    }

    // ////////// Iterator ////////////

    // Return an iterator that will visit all
    // elements of this list, in left-to-right order.
    @Override
    public Iterator<E> iterator() {
        return new LRIterator();
    }

    //////////// Inner class ////////////
    private class LRIterator implements Iterator<E> {
        // An LRIterator object is a left-to-right iterator over
        // a LinkedList<E> object.
        private Node<E> position;

        // position is a link to the node containing the next
        // element to be visited.
        private LRIterator() {
            position = first;
        }

        @Override
        public boolean hasNext() {
            return (position != null);
        }

        @Override
        public E next() {
            if (position == null) throw new NoSuchElementException();
            E nextElem = position.element;
            position = position.next;
            return nextElem;
        }

        @Override
        public void remove() {
            // not implemented

        }
    }
}

Summary of algorithms and time complexities:

Operation	Algorithm	Time complexity
`contains`	SLL linear search	O(n)
`add`	SLL linear search + insertion	O(n)
`remove`	SLL linear search + deletion	O(n)
`equals`	pairwise comparison	O(n)
`containsAll`	variant of pairwise comparison	O(n)
`addAll`	SLL merge	O(n+n’)
`removeAll`	variant of SLL merge	O(n+n’)
`retainAll`	variant of SLL merge	O(n+n’)

Implementations of Small-Integer Sets Using boolean Arrays

If the members are known to be small integers, in the range 0...m-1, represent the set by:

a boolean array b of length m, such that b[i] is true if and only if i is a member of the set

Summary of algorithms and time complexities:

Operation	Algorithm	Time complexity
`contains`	test array element	O(1)
`add`	set array element to true	O(1)
`remove`	set array element to false	O(1)
`equals`	pairwise equality test	O(m)
`containsAll`	pairwise implication test	O(m)
`addAll`	pairwise disjunction	O(m)
`removeAll`	pairwise negation + conjunction	O(m)
`retainAll`	pairwise conjunction	O(m)

Comparison of Set Implementations

Operation	Member array representation	SLL representation	boolean array representation
`contains`	O(log n)	O(n)	O(1)
`add`	O(n)	O(n)	O(1)
`remove`	O(n)	O(n)	O(1)
`equals`	O(n)	O(n)	O(m)
`containsAll`	O(n)	O(n)	O(m)
`addAll`	O(n+n’)	O(n+n’)	O(m)
`removeAll`	O(n+n’)	O(n+n’)	O(m)
`retainAll`	O(n+n’)	O(n+n’)	O(m)

The member array representation is suitable only for small or infrequently changing sets. The SLL representation is suitable only for small sets. The boolean array representation is suitable only for sets of small integers.

For general applications, we need a more efficient set representation either a search tree or a hash-table.

Example: Information Retrieval

Consider a simple information retrieval system. A query is viewed as a set of keywords. Given a query, the system scores each document according to how many of the keywords it contains.

  
package sets;

import java.io.BufferedReader;
import java.io.FileNotFoundException;
import java.io.FileReader;
import java.io.IOException;
import java.util.Set; // using Java's own set interface here
import java.util.TreeSet; // and the implementation that uses a BST

public class InformationRetrieval {

    // method from the lecture

    public static int score(BufferedReader doc, Set<String> keywords) {
        // return the number of words in keywords
        // that are also in the document doc
        Set<String> missing = new TreeSet<String>(keywords); // uses a copy
        // constructor
        for (; ; ) {
            String line;
            try {
                line = doc.readLine();
                if (line == null) break;
                String[] words = line.split("[[^A-Z]&&[^a-z]]+");
                for (String word : words) missing.remove(word);
            } catch (IOException e) {
                // lazy auto generated catch block
                e.printStackTrace();
            }
        }
        return keywords.size() - missing.size();
    }

    public static void main(String[] args) {
        String[] niceWords = {
            "kind",
            "peaceful",
            "good",
            "safety",
            "luck",
            "happy",
            "warm",
            "generous",
            "rest",
            "mother",
            "moon",
            "friendly",
            "sleepy",
            "acceptance",
            "noble",
            "gentle",
            "grateful"
        };

        Set<String> keywords = new TreeSet<String>();
        for (String s : niceWords) keywords.add(s);
        int matches = 0;

        try {
            BufferedReader text = new BufferedReader(new FileReader("jungleBook.txt"));
            matches = score(text, keywords);

        } catch (FileNotFoundException e) {
            // another lazy catch block
            e.printStackTrace();
        }

        System.out.println("The text contains " + matches + " of the nice words");
    }
}

Week 10: Binary Search Trees

Binary-trees and binary-search-trees
Searching
Insertion
Deletion
Traversal
Implementation of sets using binary-search-trees

Binary Trees

A binary-tree consists of a header together with a number of nodes connected as follows:

each node contains an element, plus two, possibly null, links to other nodes, its left child and right child.
the header contains a ,possibly null, link to a unique node designated as the binary-tree’s root node.

A leaf node is one that has no children, both its links are null. Every node, except the root node, is the left or right child of exactly one other node, its parent. The root node has no parent, the only link to it is in the header. The size of a binary-tree is the number of nodes. An empty binary-tree has no nodes. Its header contains a null link.

Every node has a left sub-tree and a right sub-tree.

Node and Tree Depths

For any node N in a binary-tree, there is exactly one sequence of links between the root node and N. The depth of node N is the number of links between the root node and N. The depth of a binary-tree is the depth of its deepest node. A binary-tree with a single node has depth 0. By convention, an empty binary-tree has depth -1.

A binary-tree of depth d is balanced if all nodes at depths 0, 1,...,d-2 have two children.

This implies:

Nodes at depth d-1 may have two/one/no children
Nodes at depth d have no children by definition
A binary-tree of depth 0 or 1 is always balanced

Binary Search Trees

A binary-search-tree or BST is a binary-tree in which the following property holds for every node:

let elem be the element contained in the node
the node’s left sub-tree (if non-empty) contains only elements less than elem
the nodes right sub-tree (if non-empty) contains only elements greater than elem

An equivalent recursive definition of BST is also possible.

A binary-search-tree is:

empty, or
non-empty, in which case it has:
- a root node containing an element elem
- a link to a left sub-tree which (if non-empty) contains only elements less than elem
- a link to a right sub-tree which (if non-empty) contains only elements greater than elem
- where the sub-trees are themselves BST

  
package BSTs;

public class BST<E extends Comparable<E>> {
    // Each BST object is a binary-search-tree header.
    private BST.Node<E> root;

    public BST() {
        // Construct an empty BST.
        root = null;
    }

    // //////// Inner class //////////
    private static class Node<E extends Comparable<E>> {
        protected E element;
        protected Node<E> left, right;

        protected Node(E elem) {
            element = elem;
            left = null;
            right = null;
        }

        public Node<E> deleteTopmost() {
            if (this.left == null) return this.right;
            else if (this.right == null) return this.left;
            else { // this node has two children
                this.element = this.right.getLeftmost();
                this.right = this.right.deleteLeftmost();
                return this;
            }
        }

        private E getLeftmost() {
            Node<E> curr = this;
            while (curr.left != null) curr = curr.left;
            return curr.element;
        }

        public Node<E> deleteLeftmost() {
            if (this.left == null) return this.right;
            else {
                Node<E> parent = this, curr = this.left;
                while (curr.left != null) {
                    parent = curr;
                    curr = curr.left;
                }
                parent.left = curr.right;
                return this;
            }
        }
    }

    // ///// end of inner class ///////////

    public BST.Node<E> search(E target) {
        int direction = 0;
        BST.Node<E> curr = root;
        for (; ; ) {
            if (curr == null) return null;
            direction = target.compareTo(curr.element);
            if (direction == 0) return curr;
            else if (direction < 0) curr = curr.left;
            else curr = curr.right;
        }
    }

    public void insert(E elem) {
        int direction = 0;
        BST.Node<E> parent = null, curr = root;
        for (; ; ) {
            if (curr == null) {
                BST.Node<E> ins = new BST.Node<E>(elem);
                if (root == null) root = ins;
                else if (direction < 0) parent.left = ins;
                else parent.right = ins;
                return;
            }
            direction = elem.compareTo(curr.element);
            if (direction == 0) return;
            parent = curr;
            if (direction < 0) curr = curr.left;
            else curr = curr.right;
        }
    }

    public void delete(E elem) {
        int direction = 0;
        BST.Node<E> parent = null, curr = root;
        for (; ; ) {
            if (curr == null) return;
            direction = elem.compareTo(curr.element);
            if (direction == 0) {
                BST.Node<E> del = curr.deleteTopmost();
                if (curr == root) root = del;
                else if (curr == parent.left) parent.left = del;
                else parent.right = del;
                return;
            }

            parent = curr;
            if (direction < 0) curr = parent.left;
            else
                // direction > 0
                curr = parent.right;
        }
    }

    public void printInOrder() {
        printInOrder(root);
    }

    private static <E extends Comparable<E>> void printInOrder(BST.Node<E> top) {
        // Print, in ascending order, all the elements in the BST
        // subtree whose topmost node is top.
        if (top != null) {
            printInOrder(top.left);
            System.out.println(top.element);
            printInOrder(top.right);
        }
    }

    /**
     * @param args
     */
    public static void main(String[] args) {
        BST<String> animals = new BST<String>();

        animals.insert("lion");
        animals.insert("fox");
        animals.insert("rat");
        animals.insert("cat");
        animals.insert("pig");
        animals.insert("dog");
        animals.insert("tiger");
        animals.printInOrder();
    }
}

BST Search

Problem: search for a given target value in a BST

Ideas: compare the target value with the element in the root node

If the target value is equal, the search is successful
If the target value is less, search the left sub-tree
If the target value is greater, search the right sub-tree
If the sub-tree is empty, the search is unsuccessful

BST search algorithm:

To find which if any node of a BST contains an element equal to target:

Set curr to the BST root.
Repeat:
1. If curr is null, terminate yielding null.
2. Else, if target is equal to curr.element, terminate yielding curr.
3. Else, if target is less than curr.element, set curr to curr.left.
4. Else, set curr to curr.right.

BST search efficiency is clearly related to the BST depth, but how is its depth related to its size?

A balanced BST of depth d has al least \(2^d\) and at most \(2^{d+1}-1\) nodes. Therefore, depth of balanced BST of size \(n \approx log_2(n)\).

An unbalanced BST of depth d could have as few as \(d+1\) nodes. Therefore, the maximum depth of unbalanced BST of size \(n = n-1\)

Analysis (counting comparisons):

Let the BST size be n.

If the BST has depth d, the maximum number of comparisons is \(d+1\). If the BST is balanced, \(d \approx log_2(n)\), best-case time complexity is \(O(log_2(n))\).

If the BST is unbalanced, \(d \approx n\), worst-case time complexity is \(O(n)\).

  
    public BST.Node<E> search(E target) {
        int direction = 0;
        BST.Node<E> curr = root;
        for (; ; ) {
            if (curr == null) return null;
            direction = target.compareTo(curr.element);
            if (direction == 0) return curr;
            else if (direction < 0) curr = curr.left;
            else curr = curr.right;
        }
    }

BST Insertion

Problem: insert a new element into a BST

We must create a new node, but we must link the new node to the BST in such a way that it remains a BST.

Ideas: proceed as if searching for that element. If the element is not already present, the search will lead to a null link. Replace that null link by a link to a leaf node containing the new element.

BST insertion algorithm:

To insert the element elem into a BST:

Set parent to null, and set curr to the BST root.
Repeat:
1. If curr is null:
  1. Replace the null link from which curr was taken, either the BST root or parent’s left child or right child, by a link to a newly created leaf node with element elem.
  2. Terminate.
2. Else, if elem is equal to curr’s element, Terminate.
3. Else, if elem is less than curr’s element, set parent to curr, set curr to its left child.
4. Else, set parent to curr, set curr to its right child.

Analysis (counting comparisons):

Number of comparisons is the same as for BST search.

If the BST is balanced, best-case time complexity is \(O(log_2(n))\).

If the BST is unbalanced, worst-case time complexity is \(O(n)\).

BST Deletion

Problem: delete a given element from a BST.

Idea: search for the given element. Then delete the node containing it. If that node has one child or none, deleting it is easy. But if that node has two children, we must take care not to leave two disconnected sub-trees.

BST deletion algorithm:

To delete the element elem in a BST:

Set parent to null, set curr to the BST root node.
Repeat:
1. if curr is null, terminate.
2. Else, if elem is equal to curr’s element:
  1. Delete the topmost element in the sub-tree whose topmost node is curr, and let del be a link to the remaining sub-tree.
  2. Replace the link to curr by del.
  3. Terminate.
3. Else, if elem is less than curr’s element, set parent to curr, and set curr to curr’s left child.
4. Else, if elem is greater than curr’s element, set parent to curr, and set curr to curr’s right child.

Delete the topmost element

Problem: delete the topmost element in a BST sub-tree.

Four cases to consider:

The topmost node has no children.
The topmost node has a right child but no left child.
Discard the topmost node, but retain a link to its right sub-tree.
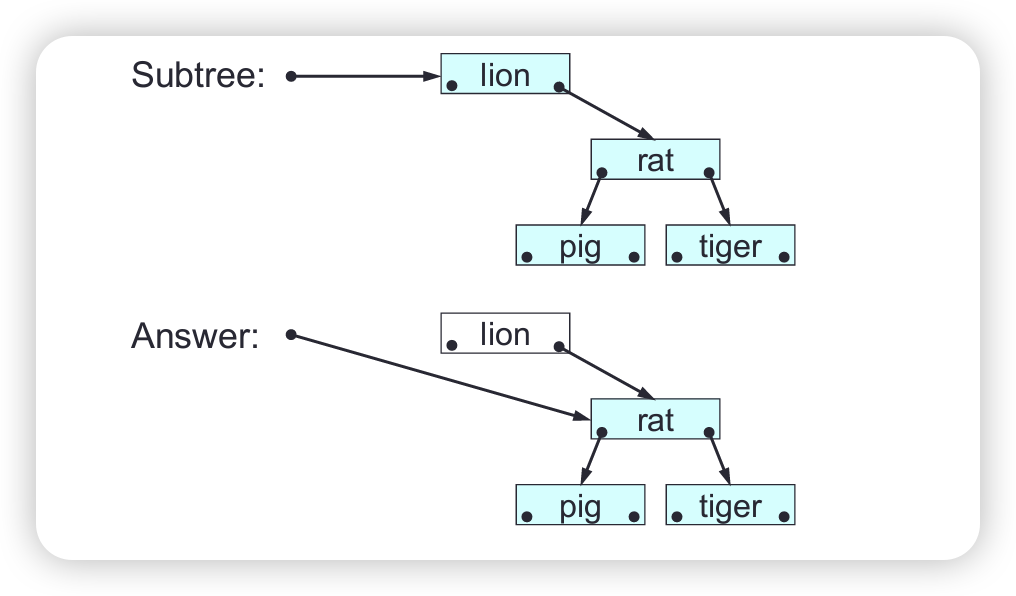
The topmost node has a left child but not right child.
Discard the topmost node, but retain a link to its left sub-tree.
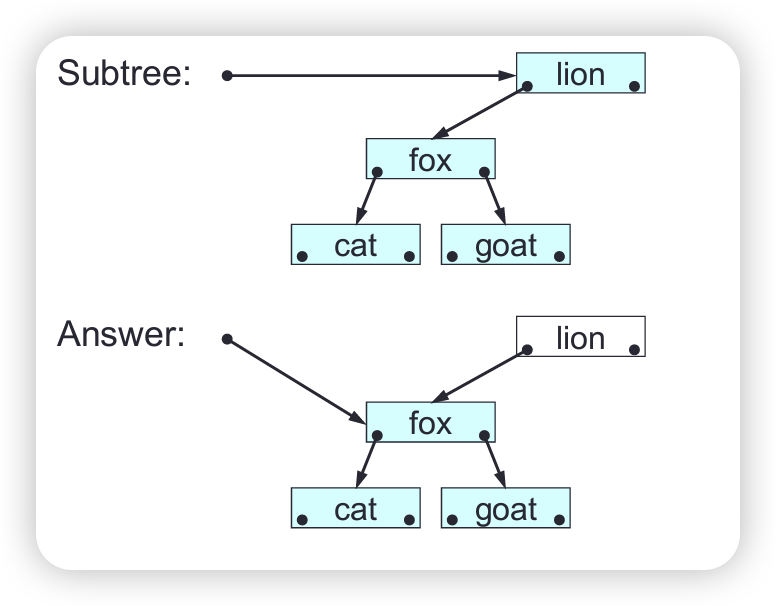
The topmost node has two children.
Copy the right sub-tree’s leftmost element into the topmost node, then delete the right sub-tree’s leftmost element.

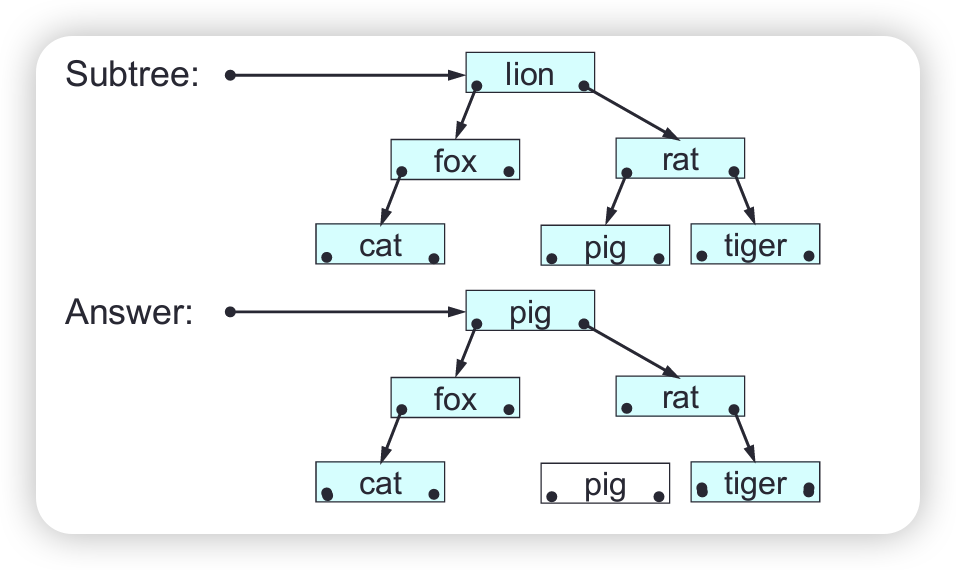
To delete the topmost element in the sub-tree whose topmost node is top:

If top has no left child, terminate with top right child as answer.
If top has no right child, terminate with top left child as answer.
If top has two children:
1. Set top’s element to the leftmost element in the right sub-tree.
2. Delete the leftmost element in the right sub-tree.
3. Terminate with top as answer.

It is easy to locate the leftmost node in a sub-tree. If the sub-tree’s topmost node has no left child, the topmost node is itself the leftmost node. If the sub-tree’s topmost node does have a left child, we follow left child links until we find a node with no left child. That node is the leftmost node.

BST in Practice

Whether a BST is balanced or unbalanced depends on the order of insertions and deletions. If elements are inserted in random order, the BST will probably be roughly balanced. If elements are inserted in ascending or descending order, the BST will be unbalanced. Deletions can make a balanced BST unbalanced, or vice versa.

Binary Tree Traversal

Binary-tree traversal: visit all nodes of the binary-tree in some predetermined order.

In-order-traversal: traverse the left sub-tree, then visit the root node, then traverse the right sub-tree.
Pre-order traversal: visit the root node, then traverse the left sub-tree, then traverse the right sub-tree.
Post-order traversal: traverse the left sub-tree, then traverse the right sub-tree, then visit the root node.

These traversals all apply to BST as a special case.

In-order Traversal

Binary-tree in-order traversal algorithm:

To traverse, in in-order, the sub-tree whose topmost node is top:

If top is not null:
1. Traverse, in in-order, top’s left sub-tree.
2. Visit top.
3. Traverse, in in-order, top right sub-tree.
Terminate.

Pre-order Traversal

Binary-tree pre-order traversal algorithm:

To traverse, in pre-order, the sub-tree whose topmost node is top:

If top is not null:
1. Visit top.
2. Traverse, in pre-order, top’s left sub-tree.
3. Traverse, in pre-order, top’s right sub-tree.
Terminate.

Post-order Traversal

Binary-tree post-order traversal algorithm:

To traverse, in post-order, the sub-tree whose topmost node is top:

If top is not null:
1. Traverse, in post-order, top’s left sub-tree.
2. Traverse, in post-order, top’s right sub-tree.
3. Visit top.
Terminate.

Usage of Traversals:

In-order:

outputs elements in ascending order
infix representation of mathematical expressions

Pre-order:

to reproduce the tree

Post-order:

postfix representation of mathematical expression (reverse polish notation)
to delete the whole tree, delete nodes in post-order.

AVL Trees

See:

G.Adelson-Velskii and E.M.Landis, “An algorithm for the organization of information.” Doklady Akademii Nauk SSSR, 146:263–266, 1962 (Russian). English translation by Myron J. Ricci in Soviet Math. Doklady, 3:1259–1263, 1962.
Donald Knuth. The Art of Computer Programming, Volume 3: Sorting and Searching, Third Edition. Addison-Wesley, 1997. ISBN 0-20189685-0. Pages 458–475 of section 6.2.3: Balanced Trees. Note that Knuth calls AVL trees simply “balanced trees.”

Discovered in 1962, Adelson-Belskii and Landis trying to devise a better data structure for a chess engine. Depth ensured to be O(log n), but not always perfectly balanced. Recursive definition: the sub-trees of every node differ in height by at most one. Every sub-tree is an AVL tree. The height of an empty tree is -1, the height of a single node is 0.

Operations on AVL trees: search, insert, or delete. Insert is the same as for BST but may have to fix the tree after insertion to restore the balance condition. You can always do this via a modification known as a rotation single rotation or double rotation. The balance condition ensures that search, insert and delete operations are all O(log n) where n is the number of nodes. Balancing is O(1).

The basic idea of single rotation:

In each case:

k1 < k2
all elements in sub-tree X are smaller than k1
all elements in sub-tree Z are larger than k2
all elements in sub-tree Y are in between k1 and k2

So:

both trees are BST for the same elements
conversion of one to the other is known as a rotation

To re-balance a binary search tree rooted at r:

Applying single notation

Start with an empty AVL tree and insert values 1 to 7 in sequential order then values 8 to 15 in reverse order.

To maintain balance condition, every time you insert a new node, starting at the node just inserted, travel up tree.

if we reach root node without finding a bad node, we are done.
if we reach bad node, do a rotation and we are done.

We are balancing the deepest unbalanced node, if tree is now balanced, continue.

Let x be the deepest node where an imbalance occurs. Four cases to consider.

The insertion is in the:

left sub-tree of the left child of x, single rotation
right sub-tree of the right child of x, single rotation
right sub-tree of the left child of x, double rotation
left sub-tree of the right child of x, double rotation

How to do a double rotation:

Let k1 be the deepest node at which imbalance occurs, k2 and k3 next two nodes along the path leading to the inserted node. Then, rotate about k2 and k3, then rotate about k1 and k3.

  
package AVLTree;

public class AVL<E extends Comparable<E>> {
    // Each BST object is a binary-search-tree header.
    private AVLNode<E> root;

    public AVL() {
        // Construct an empty BST.
        root = null;
    }

    // //////// Inner class //////////
    private static class AVLNode<E extends Comparable<E>> {
        private E element;
        protected AVLNode<E> left, right;
        protected AVLNode<E> parent;
        protected int height;

        protected AVLNode(E elem) {
            element = elem;
            left = null;
            right = null;
            parent = null;
            height = 0;
        }

        protected AVLNode(E elem, AVLNode<E> p) {
            element = elem;
            left = null;
            right = null;
            parent = p;
            height = 0;
        }

        // omitting deletion

        /* set height of tree rooted at p
         *
         */
        public void setHeight(int h) {
            height = h;
        }

        /* return height of tree rooted at p
         *
         */
        public int getHeight() {
            return height;
        }

        /* get the right node
         *
         */
        public AVLNode<E> getRight() {
            return right;
        }

        /* set the right node
         *
         */
        public void setRight(AVLNode<E> p) {
            right = p;
        }

        /* get the left node
         *
         */
        public AVLNode<E> getLeft() {
            return left;
        }

        /* set the left node
         *
         */
        public void setLeft(AVLNode<E> p) {
            left = p;
        }

        public AVLNode<E> getParent() {
            return parent;
        }

        public void setParent(AVLNode<E> p) {
            parent = p;
        }

        public void switchChild(AVLNode<E> k1, AVLNode<E> k2) {
            if (right == k1) right = k2;
            else if (left == k1) left = k2;
        }

        public void resetHeight() {
            if (left == null && right == null) height = 0;
            else {
                if (left == null) {
                    right.resetHeight();
                    height = right.getHeight() + 1;
                } else {
                    if (right == null) {
                        left.resetHeight();
                        height = left.getHeight() + 1;
                    } else {
                        left.resetHeight();
                        right.resetHeight();
                        height = Math.max(left.getHeight(), right.getHeight()) + 1;
                    }
                }
            }
        }

        public AVLNode<E> sRotateLeft() {
            AVLNode<E> k1 = this;
            AVLNode<E> k2 = right;
            k1.setRight(k2.getLeft());
            k2.setLeft(k1);
            k2.resetHeight(); // this will reset k1 too as it is a child of k2
            k1.getParent().switchChild(k1, k2);
            k1.setParent(k2);
            return k2;
        }

        public AVLNode<E> sRotateRight() {
            AVLNode<E> k1 = this;
            AVLNode<E> k2 = left;
            k1.setLeft(k2.getRight());
            k2.setRight(k1);
            k2.resetHeight(); // this will reset k1 too as it is a child of k2
            k1.getParent().switchChild(k1, k2);
            k1.setParent(k2);
            return k2;
        }

        public AVLNode<E> dRotateLeftRight() {
            AVLNode<E> k1 = this;
            AVLNode<E> k2 = left;
            AVLNode<E> k3 = k2.getRight();
            k1.setLeft(k2.sRotateLeft());
            k1.sRotateRight();
            return k3;
        }

        public AVLNode<E> dRotateRightLeft() {
            AVLNode<E> k1 = this;
            AVLNode<E> k2 = right;
            AVLNode<E> k3 = k2.getLeft();
            k1.setRight(k2.sRotateRight());
            k1.sRotateLeft();
            return k3;
        }

        // is the node unbalanced?
        // return -1 if too heavy to the left
        // return 1 if too heavy to the right
        public int isUnbalanced() {
            // to finish

            return -1;
        }
    }

    // include method - return a node k1 (or null)
    // if non - null, is the deepest unbalanced node
    // has adding this node caused an imbalance in the tree?
    // do I need to know what my parent is to do this?

    //

    // ///// end of inner class ///////////

    public AVLNode<E> search(E target) {
        // unchanged from BST
        int direction = 0;
        AVLNode<E> curr = root;
        for (; ; ) {
            if (curr == null) return null;
            direction = target.compareTo(curr.element);
            if (direction == 0) return curr;
            else if (direction < 0) curr = curr.left;
            else curr = curr.right;
        }
    }

    public void insert(E elem) {
        int direction = 0;
        AVLNode<E> parent = null, curr = root;
        for (; ; ) {
            if (curr == null) {
                AVLNode<E> ins = new AVLNode<E>(elem);
                if (root == null) root = ins;
                else if (direction < 0) parent.left = ins;
                else parent.right = ins;
                ins.setParent(parent);
                root.resetHeight();
                rebalance(ins);
                return;
            }
            direction = elem.compareTo(curr.element);
            if (direction == 0) return;
            parent = curr;
            if (direction < 0) curr = curr.left;
            else curr = curr.right;
        }
    }

    // rebalance if necessary from inserted node ins
    public void rebalance(AVLNode<E> ins) {
        AVLNode<E> curr = ins;
        int childDirection = 1; // to the right
        int grandchildDirection = 1; // to the right
        while (curr != root) {
            // work back up the tree, ins itself is never unbalanced
            curr = curr.getParent();
        }
    }

    // omit deletion

    public void printInOrder() {
        printInOrder(root);
    }

    // added this so that I can see whether the balancing has worked ok
    public void printPreOrder() {
        printPreOrder(root);
    }

    /*
     * return the height of the node p
     */
    private static <E extends Comparable<E>> int getHeight(AVLNode<E> p) {
        return p.getHeight();
    }

    /*reset the heights of all the nodes starting at p
     *
     */
    public static <E extends Comparable<E>> void resetHeights(AVLNode<E> p) {}

    private static <E extends Comparable<E>> void printInOrder(AVLNode<E> top) {
        // Print, in ascending order, all the elements in the BST
        // subtree whose topmost node is top.
        if (top != null) {
            printInOrder(top.left);
            System.out.println(top.element);
            printInOrder(top.right);
        }
    }

    private static <E extends Comparable<E>> void printPreOrder(AVLNode<E> top) {
        // Print, in ascending order, all the elements in the BST
        // subtree whose topmost node is top.
        if (top != null) {
            System.out.println(top.element);
            printInOrder(top.left);
            printInOrder(top.right);
        }
    }

    /**
     * @param args
     */
    public static void main(String[] args) {
        AVL<String> animals = new AVL<String>();

        animals.insert("lion");
        animals.insert("fox");
        animals.insert("rat");
        animals.insert("cat");
        animals.insert("pig");
        animals.insert("dog");
        animals.insert("tiger");
        animals.printInOrder();
    }
}

When to do a rotation?

During recursive implementation of insert for AVL tree, when insertion has been performed to a left sub-tree of node p, if height of sub-trees of p differ by 2, need rotation, if the new root of left sub-tree is less than e, need a single rotation, else need a double left right rotation.

Similar argument for when insertion has been performed to a right sub-tree of node p. Only need to reset the heights of the tree when new node added, but no rotation required.

Week 11: Map

Map concepts
Map applications
A map ADT: requirements, contract
Implementation of maps: using key-indexed arrays, entry arrays, linked-lists, BST
Maps in the Java class library

Map Concepts

A map is a collection of entries, in no fixed order, in which all entries have distinct keys. Each entry is a tuple that consists of a key field and a value field. More generally, an entry is a tuple consisting of one or more key fields and one or more value fields.

The size or cardinality of a map m is the number of entries in m. This is written #m, such as #NAFTA = 3. An empty map has no entries. We can lookup a map for a given key, to obtain the corresponding value. For example, looking up NAFTA for US gives “dollar,” looking up NAFTA for UK gives nothing.

We can overlay map m1 by map m2. The result contains all entries from both m1 and m2, except that where both maps contain entries with the same key, the result contains the entry from m2 only.

Map Applications

Relational databases (RDB), An RDB table is a collection of tuples, in no particular order. If an RDB table has a key field, all tuples must have distinct keys. So an RDB relation with a key field is in fact a map.

Phone book, each entry consists of a name, address, and phone number. Several entries may share the same name or the same address, but each entry must have a unique name-and-address combination. The entries could be in any order, thus a phone book is a map in which the key field is the name-and-address combination.

  
package maps;

import java.util.Iterator;
import java.util.Scanner;
import java.util.TreeMap;

public class MobilePhone {
    private java.util.Map<String, String> contacts; // not our interface, java.util's
    // This is the table of contacts. Each entry consists of
    // a name and a phone number (both strings).
    private Iterator<String> names;
    private String currentName = "???";
    static Scanner input = new Scanner(System.in);

    public MobilePhone() {
        contacts = new TreeMap<String, String>();
    }

    public void addContact() {
        // Add a new contact, consisting of a name and
        // phone number entered by the user.

        String newName = Keypad.readName();
        String newNum = Keypad.readNumber();
        String oldNum = contacts.get(newName);
        if (oldNum != null) {
            System.out.println("Do you really want to replace the number for " + newName + "?\n");
            System.out.println("Type Y or N");
            String answer = input.next();
            if (answer.equals("N")) addContact();
        }
        contacts.put(newName, newNum);
    }

    public void displayFirstContact() {
        // Display the first contact's name.
        names = contacts.keySet().iterator();
        displayNextContact();
    }

    public void displayNextContact() {
        // Display the next contact's name.
        if (names.hasNext()) currentName = names.next();
        else currentName = "???";
        Display.write(currentName);
    }

    public void callContact() {
        // Make a call to the currently displayed contact.
        String num = contacts.get(currentName);
        if (num != null) {
            Display.write(num);
            // ... Make a call to num.

        }
    }

    public void removeContact() {
        // Remove the currently displayed contact.
        contacts.remove(currentName);
    }

    public void outputContacts() {
        System.out.println(contacts.toString());
    }

    private static class Keypad {
        public static String readName() {
            System.out.println("Input name followed by return: ");

            String name = input.next();
            // input.nextLine();
            // input.close();
            return name;
        }

        public static String readNumber() {

            System.out.println("Input number followed by return: ");

            String number = input.next();

            return number;
        }
    }

    private static class Display {
        public static void write(String s) {
            System.out.println(s);
            System.out.println("Calling " + s);
            System.out.println("Press return to end call");

            input.next();
        }
    }

    public static void main(String[] args) {
        // testing the mobile phone class

        MobilePhone myPhone = new MobilePhone();
        myPhone.addContact();
        myPhone.addContact();
        myPhone.addContact();
        myPhone.outputContacts();
    }
}

A map ADT: requirements, contract

Requirements

it must be possible to make a map empty
it must be possible to test whether a map is empty
it must be possible to test whether a map contains an entry with a given key
it must be possible to look up the value corresponding to a given key in a map
it must be possible to add a new entry to a map or to replace an existing entry
it must be possible to remove an entry from a map, given its key
it must be possible to test whether two maps are equal
it must be possible to compute the overlay of two maps
it must be possible to traverse a map

Contract

  
package maps;

import java.util.Set;

public interface Map<K, V> {
    // Each Map<K,V> object is a homogeneous map
    // whose keys and values are of types K and V
    // respectively.
    //////////// Accessors ////////////
    public boolean isEmpty();

    // Return true if and only if this map is empty.
    public int size();

    // Return the size of this map.
    public V get(K key);

    // Return the value in the entry with key in this map,
    // or null if there is no such entry.
    public boolean equals(Map<K, V> that);

    // Return true if this map is equal to that.
    public Set<K> keySet();

    // Return the set of all keys in this map.
    //////////// Transformers ////////////
    public void clear();

    // Make this map empty.
    public V remove(K key);

    // Remove the entry with key (if any) from this map.
    // Return the value in that entry, or null if there was
    // no such entry.
    public V put(K key, V val);

    // Add the entry (key, val) to this map, replacing any
    // existing entry whose key is key. Return the value in
    // that entry, or null if there was no such entry.
    public void putAll(Map<K, V> that);
    // Overlay this map with that, i.e., add all entries of
    // that to this map, replacing any existing entries
    // with the same keys.

}

Implementation of maps

Using Key-Indexed Arrays

If the keys are known to be small integers, in the range 0...m-1, represent the map by:

an array vals of length m, such that vals[k] contains a value v if and only if (k,v) is an entry of the map.

Operation	Algorithm	Time Complexity
`get`	inspect array element	O(1)
`remove`	make array element null	O(1)
`put`	update array element	O(1)
`putAll`	pairwise update all array elements	O(m)
`equals`	pairwise equality test	O(m)

Using Entry Arrays

Represent a bounded map, size <= cap, by:

a variable size
an array entries of length cap, containing the map entries in entries[0...size-1], which is kept sorted by key.

Operation	Algorithm	Time Complexity
`get`	binary search	O(log n)
`remove`	binary search, then array deletion	O(n)
`put`	binary search, then array insertion	O(n)
`putAll`	variant of array merge	O(n + n’)
`equals`	pairwise equality test	O(n’)

  
package maps;

import java.util.Set;
import java.util.TreeSet;

public class ArrayMap<K extends Comparable<K>, V extends Comparable<V>> implements Map<K, V> {
    private Entry<K, V>[] entries;
    private int card; // cardinality of the map (number of non-null entries)

    /// constructor ////
    @SuppressWarnings("unchecked")
    public ArrayMap(int maxCard) {
        // construct a map, initially empty,whose cardinality
        // will be bounded by maxCard
        entries = (Entry<K, V>[]) new Object[maxCard];
        card = 0;
    }

    @Override
    public boolean isEmpty() {
        // TODO Auto-generated method stub
        return card == 0;
    }

    @Override
    public int size() {
        // TODO Auto-generated method stub
        return card;
    }

    @Override
    public V get(K key) {
        // Return the value in the entry with key in this map,
        // or null if there is no such entry.
        int index = binarySearch(key);
        if (index == -1) return null;
        return entries[index].value;
    }

    // we are doing the DW trick of assuming that "that" is also an ArrayMap
    // add a cast just to make sure...
    // use pairwise equality
    // O(n)
    @Override
    public boolean equals(Map<K, V> that) {
        ArrayMap<K, V> other = (ArrayMap<K, V>) that;
        if (this.card != other.card) return false;
        for (int i = 0; i < card; i++) {
            if (!this.entries[i].equals(other.entries[i])) return false;
        }
        return true;
    }

    @Override
    public Set<K> keySet() {
        // Return the set of all keys in this map.
        TreeSet<K> theSet = new TreeSet<K>();
        for (Entry<K, V> e : entries) theSet.add(e.key);
        return null;
    }

    @Override
    public void clear() {
        card = 0;
    }

    @Override
    public V remove(K key) {
        // Remove the entry with key (if any) from this map.
        // Return the value in that entry, or null if there was
        // no such entry.
        // uses binary search + deletion (v similar to ArraySet)
        if (card == 0) return null; // do nothing if set is empty
        int index = binarySearch(key);
        if (index == -1) return null; // do nothing if it is not a member of this set
        // remove element at position index
        V tempValue = entries[index].value;
        for (int i = index; i < card - 1; i++) entries[i] = entries[i + 1];
        entries[card - 1] = null;
        card--;
        return tempValue;
    }

    @Override
    public V put(K key, V val) {
        // Add the entry (key, val) to this map, replacing any
        // existing entry whose key is key. Return the value in
        // that entry, or null if there was no such entry.
        // binary search and array insertion (v similar to ArraySet)

        int index = -1; // where to place this item, if appropriate
        if (card == 0) index = 0;
        // find the index of the element not less than key
        else {
            int l = 0, r = card - 1;

            // do binary search to find position to place
            while (l <= r) {
                int m = (l + r) / 2;
                int comp = key.compareTo(entries[m].key);
                if (comp == 0) {
                    V oldValue = entries[m].value;
                    entries[m] = new Entry<K, V>(key, val);
                    return oldValue; // element with same key is already there, replace
                } else if (comp < 0) {
                    if (m == 0) {
                        index = 0;
                        l = r + 1; // get out of the loop, will add to start of array
                    } else {
                        int comp2 = key.compareTo(entries[m - 1].key);
                        if (comp2 > 0) {
                            index = m;
                            l = r + 1; // get out of the loop, will add at position m
                        } else r = m - 1;
                    }

                } else { // must have comp>0
                    if (m == card - 1) {
                        index = card;
                        l = r + 1; // get out of the loop, will add to end of array
                    } else {
                        int comp2 = key.compareTo(entries[m + 1].key);
                        if (comp2 < 0) {
                            index = m + 1;
                            l = r + 1; // get out of the loop, will add at position m+1
                        } else l = m + 1;
                    }
                }
            }
        }
        // no existing entry with this key
        // add new entry to elems[position]
        if (card == entries.length) throw new ArrayIndexOutOfBoundsException();
        for (int i = card; i > index; i--) entries[i] = entries[i - 1];
        entries[index] = new Entry<K, V>(key, val);
        card++;
        return null;
    }

    @Override
    public void putAll(Map<K, V> that) {
        // Overlay this map with that, i.e., add all entries of
        // that to this map, replacing any existing entries
        // with the same keys.

        ArrayMap<K, V> other = (ArrayMap<K, V>) that;
        for (Entry<K, V> e : other.entries) put(e.key, e.value);
    }

    /// Inner class for map entries /////
    private static class Entry<K, V> {
        // Each Entry object is a map entry consisting of a key
        // of type K and a value, of type V
        private K key;
        private V value;

        private Entry(K key, V value) {
            this.key = key;
            this.value = value;
        }

        private boolean equals(Entry<K, V> otherEntry) {
            return (this.key.equals(otherEntry.key) && this.value.equals(otherEntry.value));
        }
    }

    /// end of inner class

    /** auxiliary method */
    public int binarySearch(K key) {
        // return position of element with given key
        // or -1 otherwise
        int position = -1;
        int l = 0, r = card - 1;
        while (l <= r) {
            int m = (l + r) / 2;
            int comp = key.compareTo(entries[m].key);
            if (comp == 0) return m;
            else if (comp < 0) r = m - 1;
            else l = m + 1;
        }
        return position;
    }
}

Using SLL

Represent an unbounded map by:

a variable size
an SLL, containing one entry per node, which is kept sorted by key.

Operation	Algorithm	Time Complexity
`get`	SLL linear search	O(n)
`remove`	SLL linear search, then deletion	O(n)
`put`	SLL linear search, then insertion	O(n)
`putAll`	variant of SLL merge	O(n + n’)
`equals`	pairwise equality test	O(n’)

  
package maps;

import java.util.Set;
import java.util.TreeSet;

public class LinkedMap<K extends Comparable<K>, V extends Comparable<V>> implements Map<K, V> {
    // Each LinkedMap object is a map in which the keys are of type K
    // and values of type V

    // This map is represented as follows: its cardinality is held in card;
    // first is a link to the first node of an SLL containing the entries.
    private Entry<K, V> first;
    private int card;

    //////////// Constructor ////////////

    public LinkedMap() {
        // Construct a map, initially empty.
        first = null;
        card = 0;
    }

    //////////// Accessors ////////////

    @Override
    public int size() {
        // Return this maps size.
        return card;
    }

    @Override
    public boolean isEmpty() {
        // Return true if and only if this map is empty.
        return (card == 0);
    }

    @Override
    public boolean equals(Map<K, V> that) {
        // need iterator first
        return false; // TEMPORARY
    }

    // Return the value in the entry with key in this map, or null if there
    // is no such entry.
    @Override
    public V get(K key) {
        K compKey = key;
        for (Entry<K, V> curr = first; curr != null; curr = curr.succ) {
            int comp = compKey.compareTo(curr.key);
            if (comp == 0) return curr.getValue();
            else if (comp < 0) break;
        }
        return null;
    }

    // Return the set of all keys in this map.
    @Override
    public Set<K> keySet() {
        Set<K> keys = new TreeSet<K>();
        for (Entry<K, V> curr = first; curr != null; curr = curr.succ) {
            keys.add(curr.key);
        }
        return keys;
    }

    @Override
    public String toString() {
        String temp = "";
        for (Entry<K, V> curr = first; curr != null; curr = curr.succ) {
            if (curr != first) temp += ",";
            temp += "<" + curr.key + "," + curr.value + ">";
        }
        return "{" + temp + "}";
    }

    //////////// Transformers ////////////

    @Override
    public void clear() {
        // Make this map empty.
        first = null;
        card = 0;
    }

    // Add the entry (key, val) to this map, replacing any
    // existing entry whose key is key. Return the value in
    // that entry, or null if there was no such entry.
    @Override
    public V put(K key, V val) {
        K compKey = key;
        Entry<K, V> curr, prev = null;
        for (curr = first; curr != null; curr = curr.succ) {
            int comp = compKey.compareTo(curr.key);
            if (comp == 0) {
                V oldVal = curr.value;
                curr.value = val;
                return oldVal;
            } else if (comp < 0) break;
            prev = curr;
        }
        Entry<K, V> ins = new Entry<K, V>(compKey, val, curr);
        if (prev != null) prev.succ = ins;
        else first = ins;
        card++;
        return null;
    }

    // Overlay this map with that, i.e., add all entries of
    // that to this map, replacing any existing entries
    // with the same keys.
    @Override
    public void putAll(Map<K, V> that) {
        LinkedMap<K, V> other = (LinkedMap<K, V>) that;
        this.overlay(other);
    }

    private void overlay(LinkedMap<K, V> that) {
        // Overlays all entries of that map into this map.
        Entry<K, V> prev = null;
        int comp;
        for (Entry<K, V> cur1 = this.first, cur2 = that.first; cur1 != null || cur2 != null; ) {
            if (cur1 == null) comp = +1;
            else if (cur2 == null) comp = -1;
            else {
                comp = (cur1.key).compareTo(cur2.key);
            }
            if (comp == 0) {
                cur1.value = cur2.value;
                cur2 = cur2.succ;
            } else if (comp > 0) {
                // Insert cur2.element into this map ...
                Entry<K, V> ins = new Entry<K, V>(cur2.key, cur2.value, cur1);
                if (prev == null) this.first = ins;
                else prev.succ = ins;
                cur2 = cur2.succ;
            }
            prev = cur1;
            cur1 = cur1.succ;
        }
    }

    // Remove the entry with key (if any) from this map.
    // Return the value in that entry, or null if there was
    // no such entry.
    @Override
    public V remove(K key) {
        if (key instanceof Comparable) {
            K compKey = key;
            Entry<K, V> curr, prev = null;
            for (curr = first; curr != null; curr = curr.succ) {
                int comp = compKey.compareTo(curr.key);
                if (comp == 0) {
                    if (prev != null) prev.succ = curr.succ;
                    else first = curr.succ;
                    card--;
                    return curr.value;
                } else if (comp < 0) break;
                prev = curr;
            }
        }
        return null;
    }

    //////////// Inner class for map entries ////////////

    private static class Entry<K, V> {

        // Each ArrayMap.Entry object is a map entry consisting of a key,
        // which is a Comparable object, a value, which is an arbitrary
        // object, and a link to the next entry in the SLL.
        private K key;
        private V value;
        private Entry<K, V> succ;

        private Entry(K key, V value, Entry<K, V> succ) {
            this.key = key;
            this.value = value;
            this.succ = succ;
        }

        @SuppressWarnings("unused")
        public K getKey() {
            // Return the key of this entry.
            return this.key;
        }

        public V getValue() {
            // Return the value of this entry.
            return this.value;
        }

        @SuppressWarnings("unused")
        public void setValue(V val) {
            // Update the value of this entry to be val.
            this.value = val;
        }
    }
}

Using BST

Represent an unbounded map by:

a variable size
a BST, containing one entry per node, in which the entries are ordered by their keys.

Operation	Algorithm	Time Complexity (Best)	Time Complexity (Worst)
`get`	BST search	O(log n)	O(n)
`remove`	BST deletion	O(log n)	O(n)
`put`	BST insertion	O(log n)	O(n)
`putAll`	BST merge	O(n’ log(n+n’))	O(n’n)
`equals`	traversal & search	O(n’ log n)	O(n’n)

Summary of map implementations

Operation	Key-indexed Array Representation	Entry Array Representation	SLL Representation	BST Representation
`get`	O(1)	O(log n)	O(n)	O(log n) - O(n)
`remove`	O(1)	O(n)	O(n)	O(log n) - O(n)
`put`	O(1)	O(n)	O(n)	O(log n) - O(n)
`putAll`	O(m)	O(n+n’)	O(n+n’)	O(n’log(n+n’)) - O(n’n)
`equals`	O(m)	O(n’)	O(n’)	O(n’log n) - O(n’n)

Week 12: Hash-Table

Hash-table principles
Searching
Insertion
Deletion
Hash-table design
Implementation of sets and maps using hash-tables

Hash-table Principles

If a map’s key are small integers, we can represent the map by a key-indexed array. Search, insertion, and deletion are then O(1). We can approach this performance with keys of any type.

Idea: translate each key to a small integer, and then use that integer to index any array. This is called hashing.

A hash-table is an array of m buckets, together with a hash function hash(k) that translates each key k to a bucket index in range 0...m-1.

Each key k has a home bucket in the hash-table, namely the bucket with index hash(k). To insert a new entry with key k into the hash-table, assign that entry to k’s home bucket. If k’s home bucket is already occupied, we have a collision. This must be resolved somehow. To search for an entry with key k in the hash-table, look in k’s home bucket. To delete an entry with key k from the hash-table, look in k’s home bucket.

The hash function must be consistent, k1 = k2 implies that hash(k1) = hash(k2). In general, the hash function is many-to-one. Therefore different keys may share the same home bucket, k1 != k2 but hash(k1) = hash(k2). If this actually happens, it is called a collision. Always prefer a hash function that is likely to make collisions infrequent.

Example: a hash function for words:

Suppose that keys are English words. A possible hash function:

m=26
hash(k) = (initial letter of k) - 'a'

All words with initial letter a share bucket 0;...;, all words with initial letter z share bucket 25.

Closed-bucket Hash-table

Simplest implementation of a CBHT: each bucket is an SLL. In the following illustrations, the keys are names of chemical elements. Assume:

m = 26
hash(k) = (initial letter of k) - 'a'

  
package hashtables;

public class CBHT<K, V> {
    private Node<K, V>[] buckets;

    @SuppressWarnings("unchecked")
    public CBHT(int m) {
        buckets = (Node<K, V>[]) new Node<?, ?>[m];
    }

    private int hash(K key) {
        return Math.abs(key.hashCode()) % buckets.length;
    }

    //////// Inner class ////////
    private static class Node<K, V> {
        // Each Node object is a node of a CBHT.
        private K key;
        private V value;
        private Node<K, V> next;

        private Node(K key, V val, Node<K, V> next) {
            this.key = key;
            this.value = val;
            this.next = next;
        }
    }

    public Node<K, V> search(K targetKey) {
        int b = hash(targetKey);
        Node<K, V> curr = buckets[b];
        while (curr != null) {
            if (targetKey.equals(curr.key)) return curr;
            curr = curr.next;
        }
        return null;
    }

    public void insert(K key, V val) {
        int b = hash(key);
        Node<K, V> curr = buckets[b];
        while (curr != null) {
            if (key.equals(curr.key)) {
                curr.value = val;
                return;
            }
            curr = curr.next;
        }
        buckets[b] = new Node<K, V>(key, val, buckets[b]);
    }

    public void delete(K key) {
        int b = hash(key);
        Node<K, V> pred = null, curr = buckets[b];
        while (curr != null) {
            if (key.equals(curr.key)) {
                if (pred == null) buckets[b] = curr.next;
                else pred.next = curr.next;
                return;
            }
            pred = curr;
            curr = curr.next;
        }
    }

    public String toString() {
        String s = "";
        for (int i = 0; i < buckets.length; i++) {
            Node<K, V> curr = buckets[i];

            while (curr != null) {
                s += "(" + curr.key + "," + curr.value + "), ";
                curr = curr.next;
            }
            s += "\n";
        }
        return s;
    }
}

public class CHBTTest {

    public static void main(String[] args) {
        CBHT<String, Integer> myTable = new CBHT<String, Integer>(10);

        myTable.insert("Ann", 20);
        myTable.insert("Bob", 22);
        myTable.insert("Edward", 22);
        myTable.insert("Susan", 21);
        myTable.insert("Mary", 21);
        myTable.insert("Peter", 21);
        myTable.insert("William", 23);
        myTable.insert("Nigel", 23);
        myTable.insert("Diane", 22);
        myTable.insert("Keith", 20);
        myTable.insert("Roland", 20);
        myTable.insert("Louise", 22);
        myTable.insert("Olive", 21);
        myTable.insert("Bill", 21);
        myTable.insert("Nina", 22);
        myTable.insert("April", 20);
        myTable.insert("Jeremy", 22);
        myTable.insert("Tim", 21);

        System.out.println(myTable);
    }
}

CBHT search algorithm:

To find which if any node of a CBHT contains an entry whose key is equal to target-key:

Set b to hash(target-key).
Find which if any node of the SLL of bucket b contains an entry whose key is equal to target-key, and terminate with that node as answer.

Step 2 is SLL linear search.

CBHT insertion algorithm:

To add an entry whose key is equal to key to a CBHT:

Set b to hash(key).
Search bucket for any entry whose key is equal to key. If found, update entry, otherwise add new entry to front of list.
Terminate.

CBHT deletion algorithm:

To delete the entry if any whose key is equal to key from a CBHT:

Set b to hash(key).
Delete any entry if any whose key is equal to key from the SLL of bucket b.
Terminate.

Analysis:

Let the number of entries be n, in the best case, no bucket contains more than (say) 2 entries, the maximum number of comparison is 2. Best-case time complexity is O(1). In the worst case, one bucket contains all n entries, the maximum number of comparisons is n, worst-case time complexity is O(n).

CBHT design consists of choosing the number of buckets m, and the hash function hash.

Design aims:

collisions should be infrequent
entries should be distributed evenly among the buckets, such that few buckets contain more than (say) 2 entries.

Choosing the number of buckets

The load factor of a hash-table is the average number of entries per bucket, n/m. If n is roughly predictable, choose m such that the load factor is likely to stay in range 0.5...0.75. A load factor < 0.5 wastes space. A load factor > 0.75 tends to result in some buckets having many entries. Where possible, choose m to be a prime number. Typically the hash function performs modulo-m arithmetic. If m is prime, the entries are more likely to be distributed evenly over the buckets, regardless of any pattern in the keys.

Choosing the hash function

The hash function should be efficient performing new arithmetic operations. The hash function should distribute the entries evenly among the buckets, regardless of any patterns in the keys.

Possible compromise: speed up the hash function by using only part of the key. But beware of any patterns in that part of the key.

Example: a hash function for words:

Suppose that a hash-table will contain about 1000 common English words. Known patterns in the keys. Letters vary in frequency: A,E,I,N,S,T are common, Q,X,Z are uncommon. Word lengths vary in frequency, length of 4 to 8 are common, other lengths are less common.

hash(k) can depend on any of k’s letters and/or length. Consider m = 20, hash(k) has length of k-1: far too few buckets, load factor is 1000/20=50. Consider m = 26, hash(k) = initial letter of k - 'a': far too few buckets, load factor is 1000/26=38, uneven distribution. Consider m = 520, hash(k) = 26 x (length of k-1) + (first letter of k - 'a'): too few buckets, load factor is `1000/520=1.9, uneven distribution. Words of length 4 are far more common than words of length 2, so buckets 78 to 103 will be far more densely populated than buckets 26 to 51. Words with first letter ‘a’ are far more common than words with first letter ‘z’, so bucket 0, 26, 52 will be far more densely populated than buckets 25, 51, 77, etc.

Consider m = 1499, hash(k) = (weighted sum of letters of k) modulo m: good number of buckets, load factor is 1000/1499 = 0.67, reasonably even distribution.

The following trials illustrate the performance of a CBHT with m buckets. The hash function was chosen to distribute keys uniformly among the m buckets, the probability that a key is mapped to any particular bucket was 1/m. In each trial, the CBHT was loaded with a set of n randomly generated keys.

课程笔记

algorithm

This post is licensed under CC BY 4.0 by the author.

Week 1: Introduction

Logs

Logs in Java

Mathematical Properties of Logs

Dividing Down to 1

Algorithms

Example: finding a midpoint

Example: computing a GCD

Data structures

Abstract Data Types (ADT)

Week 2: Algorithms and Complexity

Principles

Efficiency analysis

How should we measure time?

Complexity analysis

O-notation

Important explanations:

Common time complexities:

Recursive algorithms

Additional material:

Week 3: Arrays

Properties

Subarrays

Sorted Arrays

Java’s Comparable Interface

Insertion

Deletion

Searching

Linear Search

Binary Search

Comparison of searching algorithms

Merging

Sorting

Selection Sort

Merge Sort

Quick Sort

Comparison of sorting algorithms

Week 4 - Linked Lists

Linked Lists

Singly Linked Lists

SLL Insertion

SLL Deletion

SLL Searching

SLL Code Example in Java

Doubly Linked Lists

DLL Traversal

DLL Delete First

DLL Delete Last

DLL Insertion

DLL Deletion

Comparison of SLL and DLL Algorithms

DLL Code Example in Java

Week 5: Abstract Data Types and Collections

Data Types

Abstract Data Types

ADT Specification

Collections

Code Examples in Java

Week 6: Stacks

Overview

Stack concepts

Stack Applications

Example: text-file reversal

Example: bracket matching

Stack ADT: requirements

Stack ADT: contract

Implementation of Stacks Using Arrays

Implementation of Stacks Using SLL

Week 7: Queues

Queue concepts

Queue applications

Example: demerging

A queue ADT: requirements, contract

Requirements

Contract

Implementations Of Queues Using Arrays

Implementations Of Queues Using SLL

Deque

Summary of Terms

Week 8: Lists

Java’s `Comparable` Interface